یه نگاه عمیق به MACD

مقدمه

اندیکاتور MACD یا همون Moving Average Convergence Divergence که توسط جرالد اپل تو سال ۱۹۷۹ طراحی شد، یکی از ابزارهای محبوب و قدرتمند تو تحلیل تکنیکاله. این اندیکاتور جزو پرکاربردترین‌هاست و اون‌قدر محبوب شده که حتی تو حوزه‌های دیگه مثل پردازش سیگنال تو علوم اعصاب یا پیش‌بینی بستری شدن در بیمارستان‌ها هم استفاده شده!

تو این مطلب، می‌خوایم کلی جزئیات، فرمول‌ها، و کاربردهای این اندیکاتور افسانه‌ای رو بررسی کنیم. اگه دوست داری بیشتر از چیزی که قبلاً در مورد MACD یاد گرفتی بدونی، این مطلب کاملاً مناسب توئه.

البته، بعضی بخش‌های این مطلب ممکنه یه خورده پیچیده باشن و مناسب همه نباشن. اگه حس کردی یه قسمتی خیلی سنگینه، راحت رد شو و فقط بخش‌هایی که برات جذابه رو بخون.

جزئیات MACD

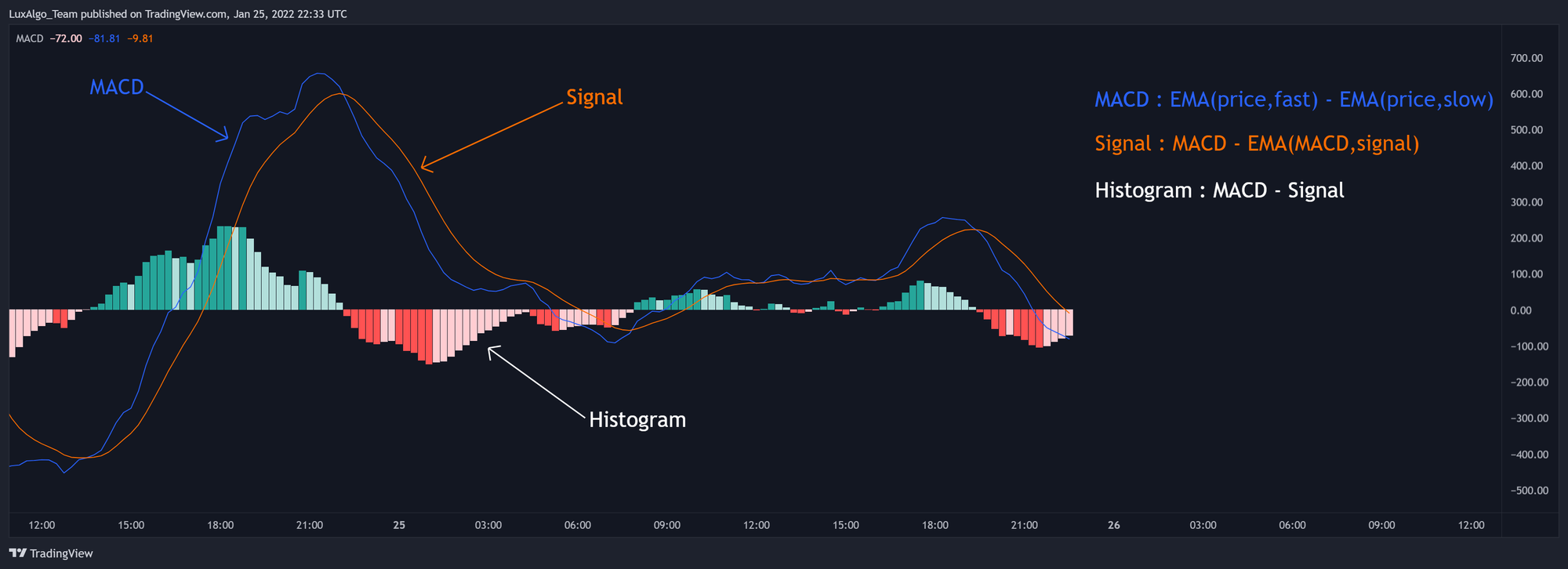
اندیکاتور MACD سه تا داده مهم بهت می‌ده:

1. MACD Line: از اختلاف بین دو میانگین متحرک نمایی (EMA) با دوره‌های زمانی مختلف به دست میاد.
2. Signal Line: این خط از میانگین متحرک نمایی خود MACD ساخته می‌شه.
3. Histogram: اختلاف بین MACD و Signal Line رو نشون می‌ده.

هر کدوم از این بخش‌ها بهت کمک می‌کنن روند فعلی بازار، مومنتوم (قدرت حرکت)، و شتاب رو تحلیل کنی. خیلی از تریدرها باور دارن اطلاعاتی که MACD ارائه می‌ده اون‌قدر کامله که می‌تونن فقط با همین ابزار ترید کنن، چه برای دنبال کردن روند بازار و چه برای معامله خلاف جهت روند.

از دید فنی و پردازش سیگنال، MACD رو می‌شه یه فیلتر Infinite Impulse Response (IIR) دونست. این فیلتر، بخش‌های فرکانس پایین و بالا رو حذف می‌کنه و هم روند رو حذف می‌کنه (detrend) و هم نمودار رو صاف‌تر نشون می‌ده.

در واقع، MACD یه سیستم خطی و ثابت در زمانه (DLTI)، یعنی همیشه به یه شکل کار می‌کنه و رفتار قابل پیش‌بینی داره.

نحوه محاسبه MACD

اندیکاتور MACD از تفاوت دو میانگین متحرک نمایی (EMA) به دست میاد:

• یکی با دوره سریع‌تر (معمولاً 12)
• یکی با دوره کندتر (معمولاً 26).

فرمول ساده‌شده به این شکله:

MACD_ = ExpMA(price, fast) - ExpMA(price, slow)

یعنی: MACD برابر با اختلاف EMA دوره سریع و EMA دوره کند هست.

فرمول دقیق‌تر

MACD رو می‌شه از یه معادله تفاضلی هم به دست آورد:

y[t] = (price[t] - price[t-1]) × g + ((1 - a1) + (1 - a2)) × y[t-1] - (1 - a1) × (1 - a2) × y[t-2]

• price[t]: قیمت فعلی
• price[t-1]: قیمت قبلی
• g: ضریب گین یا بهره
• a1 و a2: ضرایب هموارسازی EMA سریع و کند
• y[t-1] و y[t-2]: مقادیر MACD در دو دوره قبلی

محاسبه گین (g)

ضریب گین از اختلاف ضرایب هموارسازی EMA‌ها به دست میاد:

g = a1 - a2
  = 2 / (fast + 1) - 2 / (slow + 1)

• a1: ضریب EMA سریع
• a2: ضریب EMA کند

واکنش به ضربه (Impulse Response) در MACD

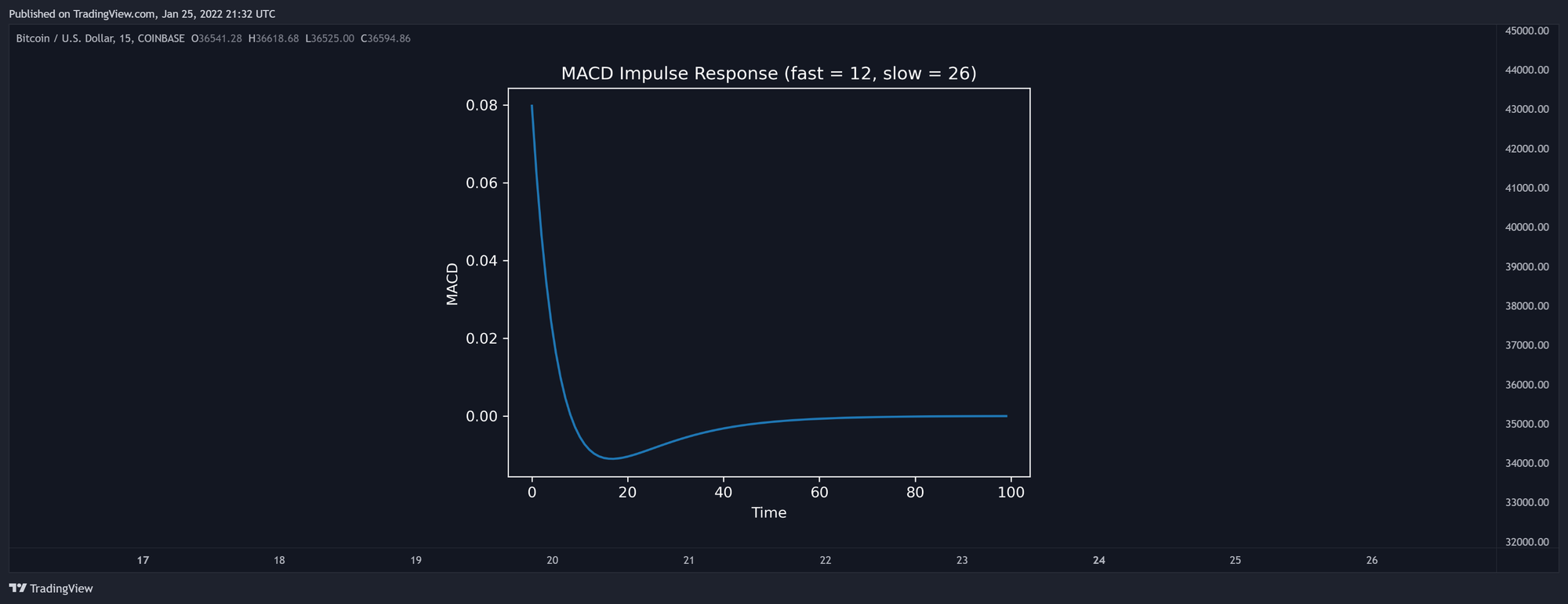
واکنش به ضربه در MACD نتیجه‌ایه که وقتی یه سیگنال ضربه واحد (یا همون تابع دلتا کرونکر) به MACD اعمال می‌کنیم، به دست میاد. تابع دلتا کرونکر اینجوری تعریف می‌شه:

d[t] = 1 if t = 0, else 0

یعنی تو لحظه صفر مقدارش ۱ هست و در بقیه زمان‌ها ۰.

تحلیل واکنش به ضربه

واکنش به ضربه، ویژگی‌های کامل MACD رو توصیف می‌کنه و از اختلاف واکنش‌های ضربه‌ای دو EMA (میانگین متحرک نمایی) با دوره‌های سریع و کند به دست میاد.

فرمول واکنش به ضربه در EMA

واکنش به ضربه یه EMA با ضریب هموارسازی aa در زمان tt به این صورته:

h(ExpMA)[t] = a × (1 - a)^t

فرمول واکنش به ضربه در MACD

برای MACD، واکنش به ضربه از اختلاف واکنش‌های ضربه‌ای دو EMA (سریع و کند) محاسبه می‌شه:

h(MACD_)[t] = a1 × (1 - a1)^t - a2 × (1 - a2)^t

• a1: ضریب هموارسازی EMA سریع
• a2: ضریب هموارسازی EMA کند

نکته مهم

مثل EMA، واکنش به ضربه در MACD هیچ‌وقت به یه حالت ثابت نمی‌رسه و تا بی‌نهایت ادامه پیدا می‌کنه. به همین خاطره که MACD به‌عنوان یه فیلتر واکنش ضربه بی‌نهایت (Infinite Impulse Response - IIR) شناخته می‌شه.

پاسخ فرکانسی (Frequency Response) در MACD

پاسخ فرکانسی به ما نشون می‌ده که یه فیلتر مثل MACD چجوری روی اجزای فرکانسی یه سیگنال تاثیر می‌ذاره. این موضوع از طریق تبدیل فوریه در زمان گسسته (DTFT) محاسبه می‌شه. توی MACD، فرمول پاسخ فرکانسی به این صورته:

H(e^iw) = SUM h[n] × e^-iwn, for n = 0 to ∞
        = SUM (a1 × (1 - a1)^n - a2 × (1 - a2)^n) × e^-iwn

• w: فرکانس زاویه‌ای که برابر 2×π×f2 \times \pi \times f هست.
• این فرمول شامل یه جمع بی‌نهایته که محاسبه مستقیمش تو عمل سخت و نشدنیه.

تابع انتقال (Transfer Function)

به‌جای محاسبه مستقیم جمع بی‌نهایت، معمولا از تابع انتقال فیلتر استفاده می‌کنیم. این تابع از تبدیل Z به دست میاد و به این صورته:

A(iw) = b[0] + b[1] × z^-iw + ... + b[p] × z^-iwP
-------------------------------------------------
B(iw) = a[0] + a[1] × z^-iw + ... + a[q] × z^-iwQ

• b: ضرایب بخش پیش‌خور (Feed-Forward Coefficients)
• a: ضرایب بخش پس‌خور (Feedback Coefficients)

این تابع برای فیلترهای خطی استفاده می‌شه و حالت کلی‌شون به این صورته:

y[t] = SUM b[p] × x[t-p] - SUM a[q] × y[t-q], for p = 0 to P & for q = 1 to Q

تابع انتقال MACD

چون MACD با معادله‌ای متفاوت تعریف شده، تابع انتقالش هم یه شکل خاص داره:

g + -g × z^-iw
----------------------------------------------------------
1 + [(a1-1) + (a2-1)] × z^-iw + [(a1-1) × (a2-1)] × z^-iw2

• g: ثابت بهره (Gain Constant) که از تفاوت ضرایب هموارسازی EMAهای سریع و کند به دست میاد.
• این تابع نشون می‌ده که MACD چجوری سیگنال رو پردازش و اجزای فرکانسی‌ش رو فیلتر می‌کنه.

محاسبه پاسخ فرکانسی

در نهایت، پاسخ فرکانسی با ارزیابی تابع انتقال برای z=eiwz = e^{iw} به دست میاد. این محاسبه توضیح می‌ده که MACD چطور اجزای فرکانسی خاصی رو تقویت یا تضعیف می‌کنه.

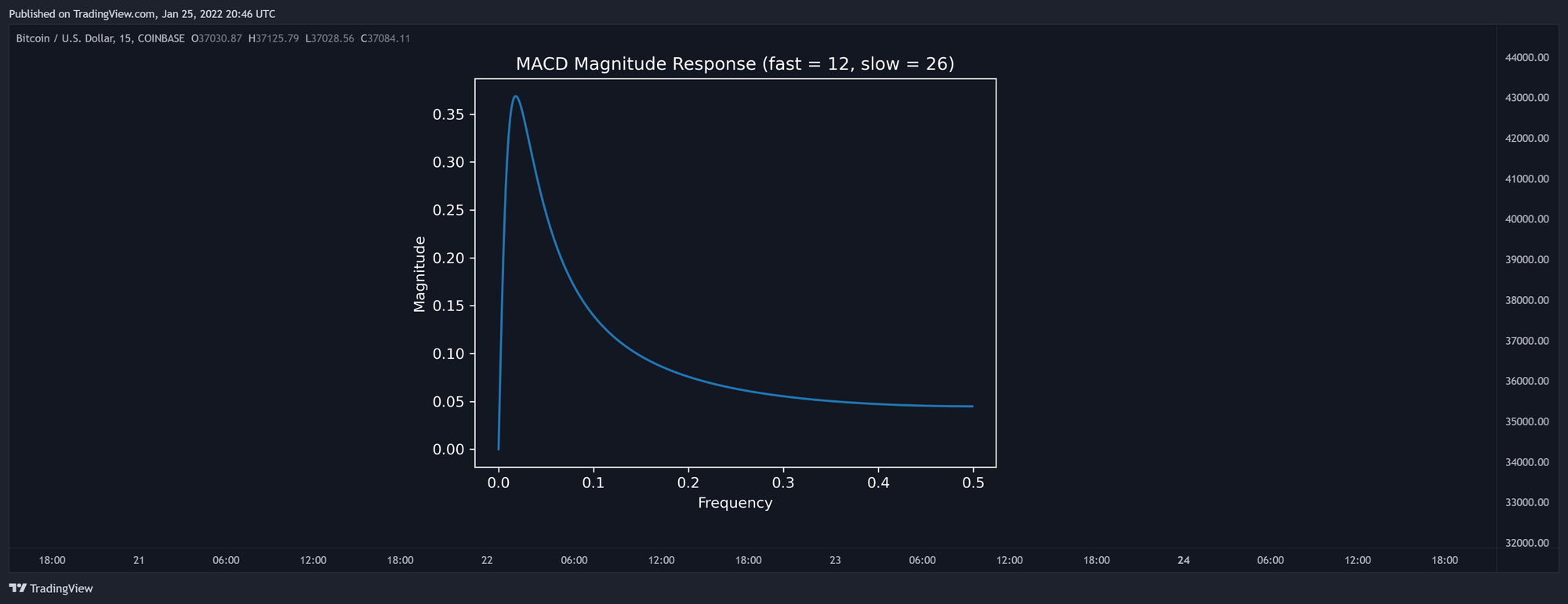
پاسخ اندازه (Magnitude Response) در MACD

پاسخ اندازه یه فیلتر نشون می‌ده که این فیلتر چطوری دامنه فرکانس‌های مختلف رو کم یا زیاد می‌کنه. این پاسخ از مقدار مطلق تابع انتقال به دست میاد که فرمولش این‌طوره:

|H(e^iw)| = sqrt(Real[H(e^iw)]^2 + Imag[H(e^iw)]^2)

فرمول بسته برای MACD

برای MACD یه فرمول دقیق به این شکل داریم:

|H(f)| = sqrt(g^2 × sin(2 × pi × f)^2 + (g - g × cos(2 × pi × f))^2) 
         ----------------------------------------------------------------------------------------------------------
         sqrt([-A1 × sin(2 × pi × f) - A2 × sin(4 × pi × f)]^2 + [A1 × cos(2 × pi × f) + A2 × cos(4 × pi × f)+1]^2)

• g: ثابت بهره (Gain Constant).
• A1 و A2: ضرایبی که از پارامترهای EMA‌های سریع (fast) و کند (slow) به دست میان:
  • A1=(a1−1)+(a2−1)A1 = (a1 - 1) + (a2 - 1)
  • A2=(a1−1)×(a2−1)A2 = (a1 - 1) × (a2 - 1)

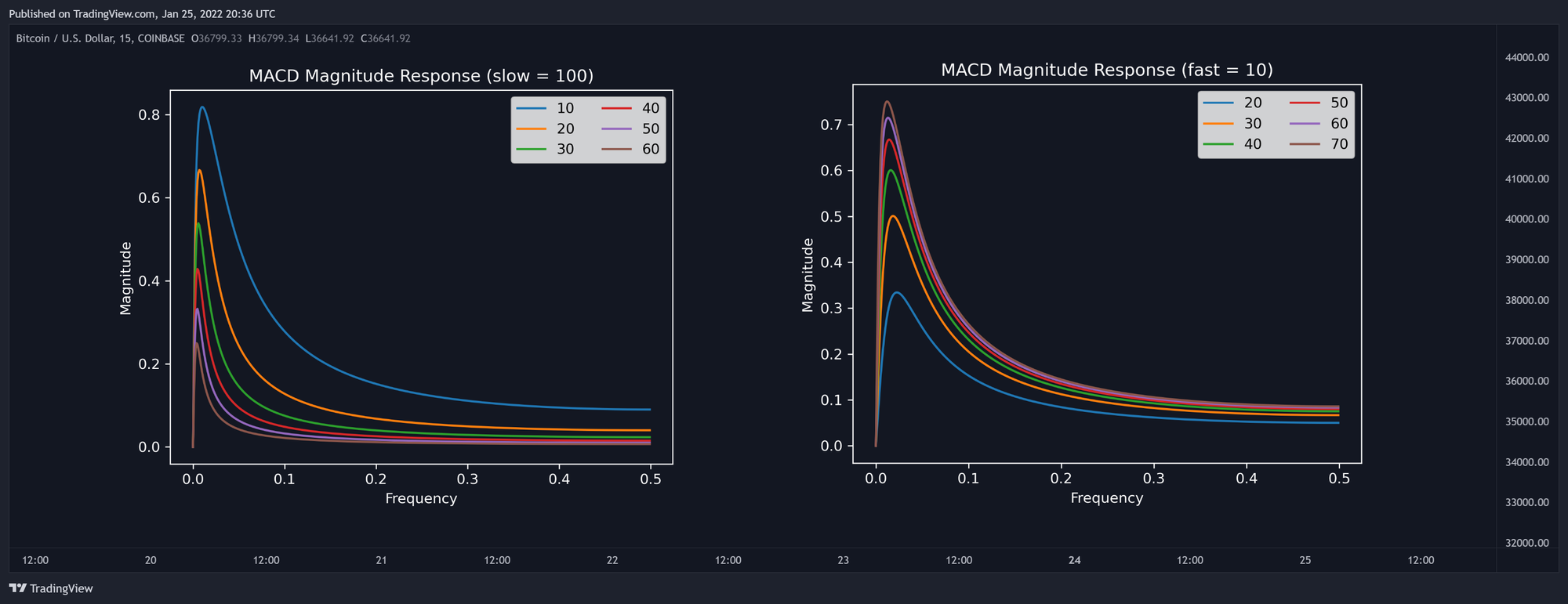
نمودار پاسخ اندازه MACD

1. شکل نامتقارن: تو نمودار، پاسخ اندازه MACD با تنظیمات پیش‌فرض (fast=12 و slow=26) نشون داده شده.
   • فرکانس‌های پایین: یه مقدار تضعیف می‌شن.
   • فرکانس‌های بالا: تضعیف کمی دارن و به خوبی فیلتر نمی‌شن.
2. تغییر تنظیمات:
   • وقتی fast نزدیک به slow باشه:
     • دامنه‌های بیشتری تو انتهای نمودار دیده می‌شه ("چاق‌تر").
     • فرکانس تشدید (جایی که کمترین تضعیف انجام می‌شه) کاهش پیدا می‌کنه.
   • وقتی slow بیشتر بشه:
     • تضعیف فرکانس‌های قوی (پیک) کمتر می‌شه.

کاربردهای MACD

MACD کاربردهای زیادی بین تریدرها داره و از روش‌های دنبال کردن روند (trend-following) تا روش‌های خلاف روند (contrarian methodologies) استفاده می‌شه.

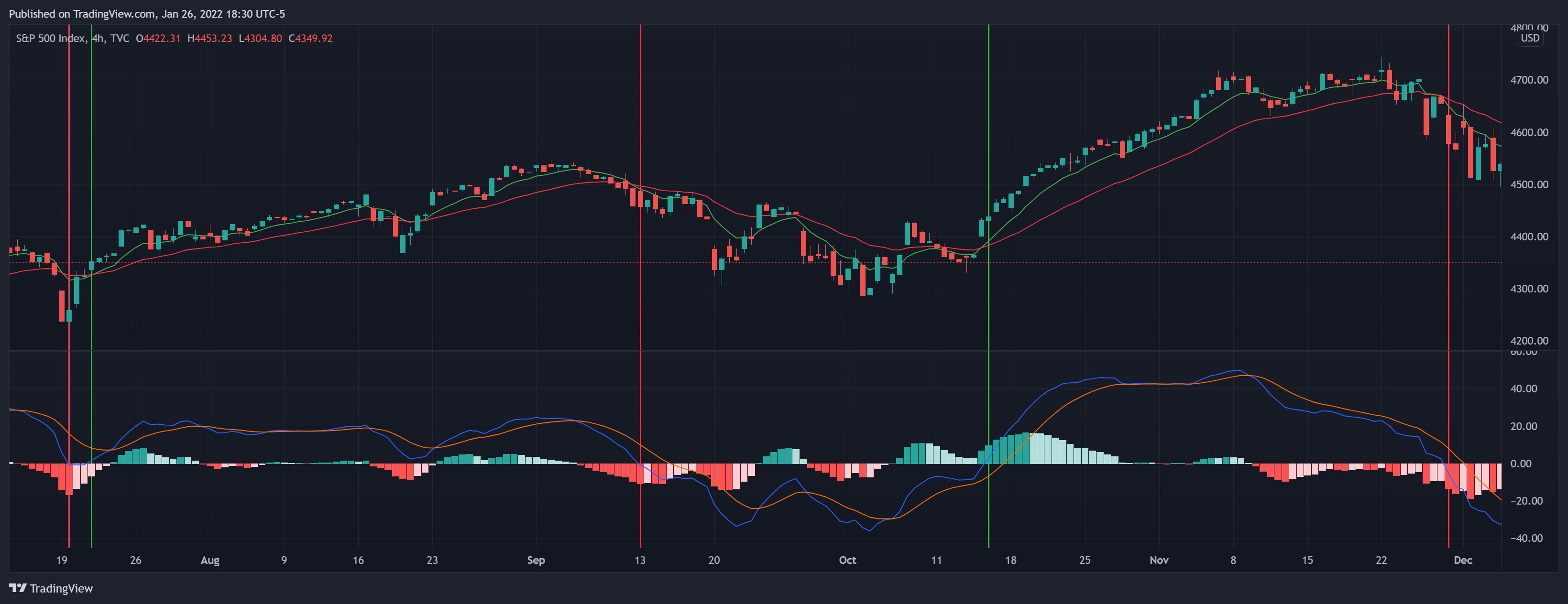
ساده‌ترین استفاده از MACD اینه که علامت MACD رو بررسی کنیم. اگر علامت مثبت باشه (یعنی میانگین متحرک نمایی سریع‌تر از میانگین متحرک نمایی کندتر باشه)، به این معنیه که بازار در حال صعوده و اگر علامت منفی باشه (میانگین متحرک نمایی سریع‌تر از میانگین متحرک نمایی کندتر کمتر باشه)، یعنی بازار در حال نزول. این روش خیلی شبیه به استراتژی ساده‌ی تقاطع میانگین‌های متحرک هست، ولی ممکنه کاربر به دلیل تأخیر زیاد این روش ساده، دچار مشکل بشه.

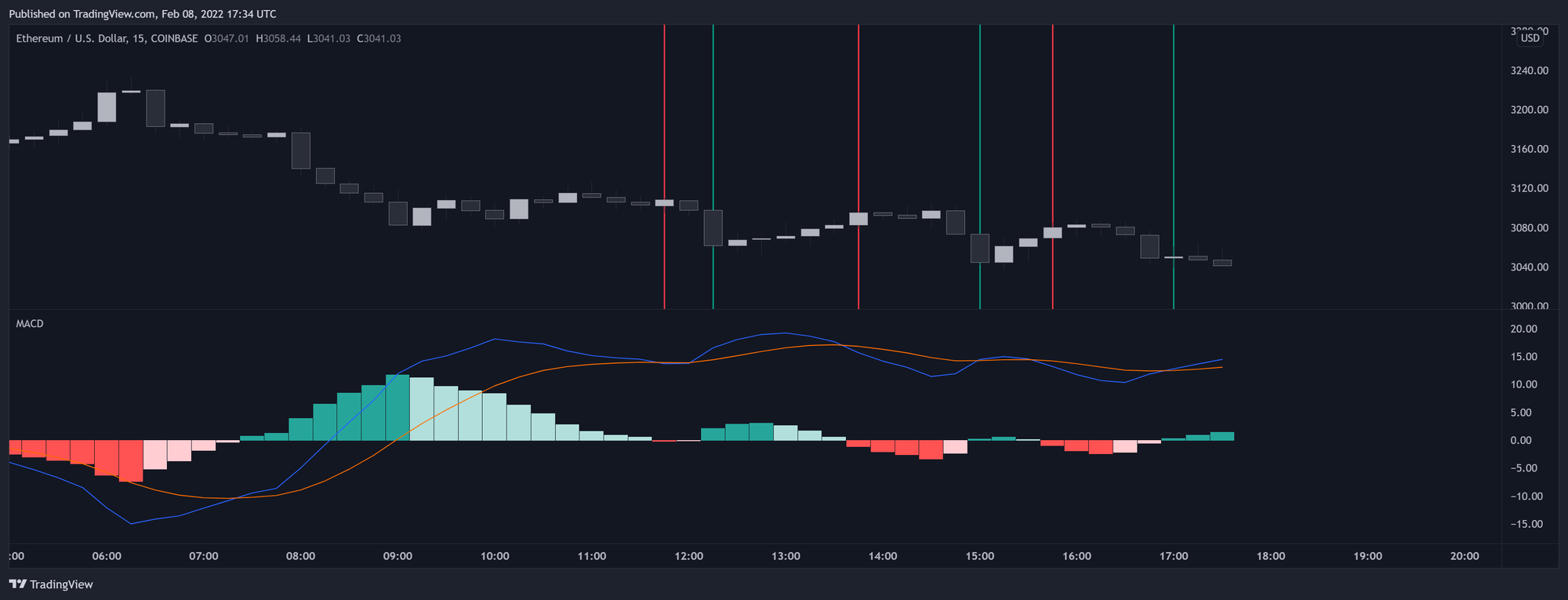
قدرت واقعی MACD وقتی مشخص می‌شه که از آن در کنار خط سیگنال و هیستوگرام استفاده بشه. برای شناسایی روندهای قیمتی به روشی به‌موقع‌تر، وقتی MACD بالای خط سیگنال باشه (هیستوگرام بالای ۰)، نشان‌دهنده‌ی روند صعودی و وقتی MACD زیر خط سیگنال باشه (هیستوگرام زیر ۰)، نشان‌دهنده‌ی روند نزولی هست. این رویکرد بهتر از ویژگی پیش‌بین‌کنندگی MACD استفاده می‌کنه و اطلاعات دقیق‌تری ارائه می‌ده. اما افزایش دقت در زمان‌بندی همیشه بی‌هزینه نیست و ممکنه به معاملات غیرمستقیم و ناپایدار (whipsaw trades) منجر بشه.

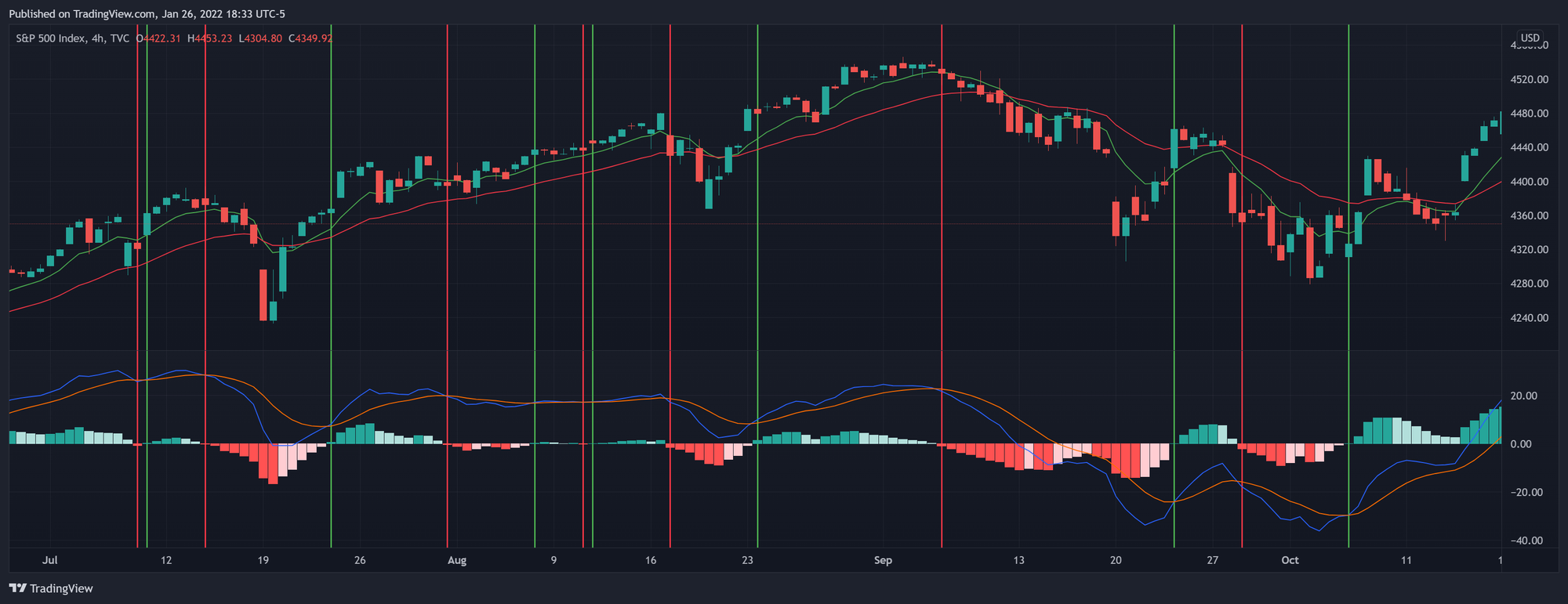
در تصویر بالا می‌بینیم که استفاده از MACD به همراه خط سیگنال باعث شناسایی سریع‌تر روندها نسبت به استفاده فقط از MACD می‌شه. همچنین می‌تونیم ببینیم که این روش حساسیت بیشتری به تغییرات قیمتی کوتاه‌مدت داره و ممکنه معاملات غیرمستقیم (whipsaw trades) رو به وجود بیاره. این موضوع به خاطر گرایش‌های مشترکی هست که اسیلاتورها برای افزایش وجود نویز در سری‌های ورودی دارن.

همچنین می‌تونیم از ترکیبی از هر دو روش استفاده کنیم تا از معایب هر کدوم جلوگیری کنیم. برای مثال، می‌تونیم معاملات رو بر اساس علامت MACD باز کنیم و وقتی MACD از خط سیگنال عبور کرد، معاملات رو ببندیم. با این حال، یکی از معایب اصلی استفاده از هیستوگرام اینه که وقتی کاربر بخواد تنظیمات اندیکاتور رو بهینه‌سازی کنه، استفاده فقط از MACD به معنای اینه که فقط دو تنظیم باید بهینه بشن، در حالی که استفاده بر اساس هیستوگرام به معنای بهینه‌سازی سه تنظیم هست که از نظر محاسباتی هزینه‌برتره.

واگرایی

واگرایی‌ها معمولاً با اسیلاتورها استفاده می‌شن. یک واگرایی زمانی اتفاق می‌افته که قیمتا در اوج یا پایین‌ترین سطح خودشون قرار می‌گیرن، اما اوج یا پایین‌ترین سطح MACD باهاشون هم‌جهت نیست. این می‌تونه نشون‌دهنده یک حرکت روند با شدت کمتر باشه که ممکنه به یک تغییر روند اشاره کنه.

دوره سریع> کند

وقتی که توی MACD، دوره‌ی سریع (Fast) خیلی بیشتر از دوره‌ی کند (Slow) باشه، این اندیکاتور می‌تونه نقاط عطف بازار رو بهتر پیش‌بینی کنه. با این حال، توانایی MACD در ارائه‌ی سیگنال‌هایی که روندهای آینده رو پیش‌بینی می‌کنن، به شرایط فعلی بازار بستگی داره. بعضی تغییرات قیمتی می‌تونن این قابلیت پیش‌بینی رو دشوار کنن. اما با تنظیم دوره‌ی سریع به گونه‌ای که خیلی بیشتر از دوره‌ی کند باشه، می‌تونیم توانایی‌های پیش‌بینی MACD رو تقویت کنیم و به سیگنال‌های دقیق‌تری دست پیدا کنیم.

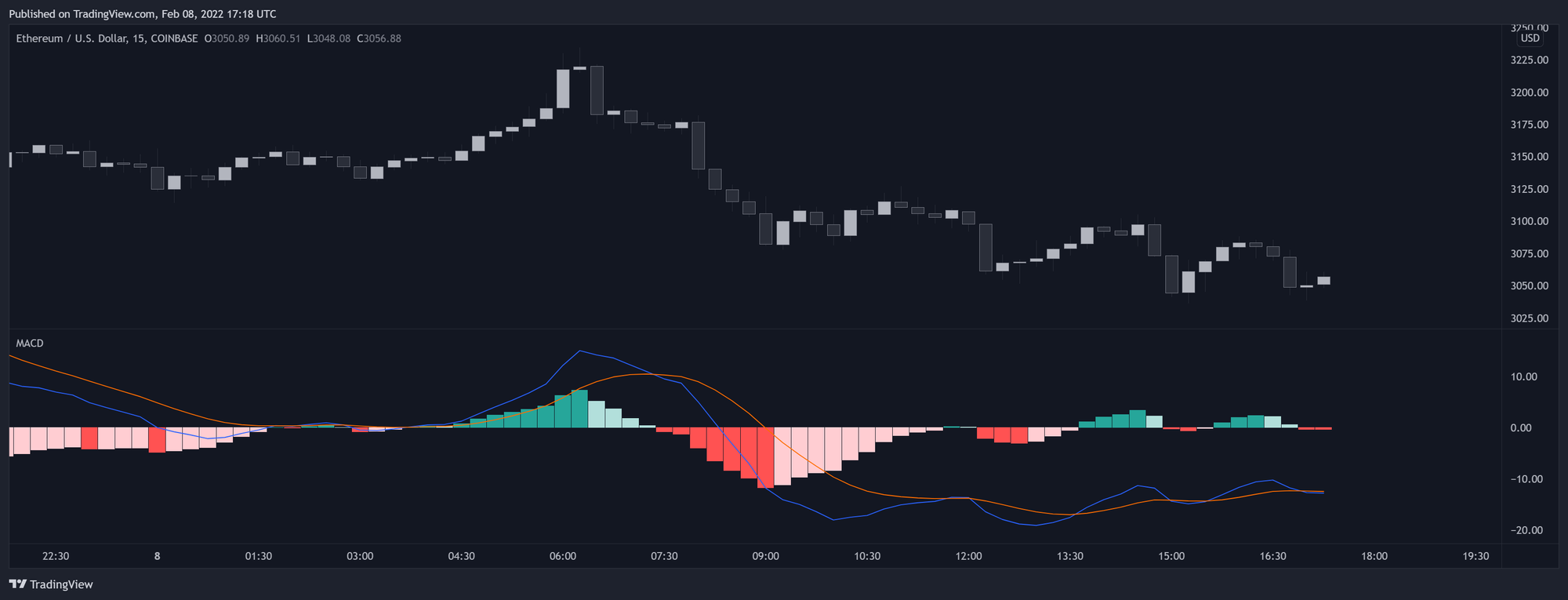
اگر کاربر از هیستوگرام MACD استفاده کنه، نوسانات دوره‌ای در یک روند قیمتی معمولاً مشکل‌ساز خواهد بود، به‌خصوص اگر طول سیگنال به‌قدری زیاد باشه که MACD رو خیلی دیر به‌روز کنه. با معکوس کردن دوره‌ی سریع و کند، میشه به سیگنال‌های زودتر از تغییرات روند رسید، به‌جای اینکه از تأخیر زیاد ناشی از هیستوگرام رنج برد. این کار می‌تونه به کاربر کمک کنه تا زودتر به تغییرات بازار واکنش نشون بده.

عملیات معکوس کردن دوره‌های سریع و کند MACD توسط "ایلر" (Ehlers) پیشنهاد شده. همچنین می‌بینیم که بهینه‌سازی تنظیمات MACD در بازارهای بازگشت به میانگین معمولاً به دوره‌های سریع بالاتر از دوره‌های کند می‌انجامد. این رویکرد بیشتر به سمت تریدرهای خلاف روند (contrarian) متمایل است. یعنی، تریدرهایی که به دنبال تغییر جهت بازار هستند و می‌خواهند از نوسانات استفاده کنن.

استفاده از MACD با انواع مختلف میانگین‌های متحرک

MACD به طور پیش‌فرض از میانگین‌های متحرک نمایی برای محاسبه میانگین‌های سریع، کند و سیگنال استفاده می‌کنه. اما می‌شه از انواع مختلف میانگین‌های متحرک هم استفاده کرد. با این کار، MACD ویژگی‌های نوع میانگین متحرک مورد استفاده رو به خود می‌گیره و ویژگی‌هایی مثل واکنش‌پذیری و نرمی رو بهبود می‌ده.

برای مثال، بعضی از کاربران ترجیح می‌دن که از میانگین متحرک ساده استفاده کنن که MACD با کمی واکنش کمتری ولی با درجه‌ای بالاتر از فیلترینگ به دست می‌ده.

استفاده از میانگین‌های متحرک با تأخیر کم هم باعث می‌شه MACD خیلی واکنش‌پذیر باشه، به طوری که هیستوگرام بتونه نقاط عطف MACD رو به خوبی پیش‌بینی کنه، چون این نوع میانگین‌های متحرک به راحتی می‌تونن سیگنال ورودی رو بیشتر یا کمتر از حد نیاز بزنند.

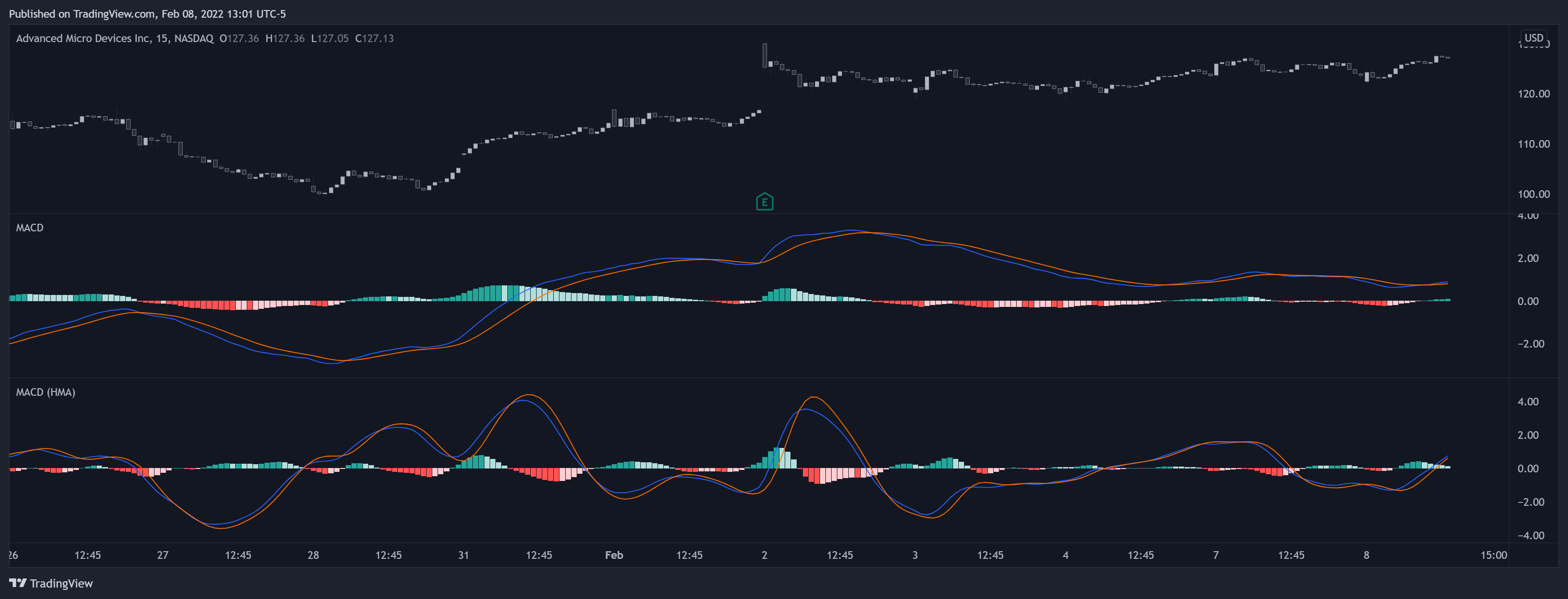
به نمودار بالا دقت کن که چطور MACD مبتنی بر میانگین متحرک هال (قسمت پایین) نسبت به یک MACD معمولی (قسمت بالا) با تنظیمات یکسان، واکنش‌پذیری بیشتری دارد. همچنین، مشاهده می‌کنی که خط سیگنال قبل از وقوع نقطه عطف MACD، می‌تواند از آن عبور کند.

با این حال، استفاده از بیش از یک نوع میانگین متحرک برای محاسبه MACD می‌تواند جالب‌تر باشد، به طوری که از نوعی میانگین متحرک که مناسب هر جزء MACD باشد، استفاده شود. به این ترتیب، داشتن یک میانگین متحرک با تأخیر کم به عنوان میانگین متحرک سریع و یک میانگین کلاسیک‌تر به عنوان میانگین متحرک کند و سیگنال می‌تواند جالب‌تر باشد.