یه نگاه عمیق به RSI

نوسان‌گرها تو تحلیل تکنیکال خیلی نقش مهمی دارن چون هم اطلاعات زیادی به ما میدن و هم می‌تونن تغییرات قیمت رو پیش‌بینی کنن. معمولاً این ابزارها رو همراه با اندیکاتورهای روند استفاده می‌کنن تا تحلیل دقیق‌تر بشه.

یکی از محبوب‌ترین نوسان‌گرها، شاخص قدرت نسبی (RSI) هست که توسط جی. ولس وایلدر طراحی شده و اولین بار تو کتاب "مفاهیم جدید در سیستم‌های معاملاتی" معرفی شده.

توی این پست قراره بریم عمیق تو دل این نوسان‌گر کلاسیک، یه سری نکته‌هاشو بررسی کنیم و همچنین اندیکاتورهای مشتق‌شده ازش رو مرور کنیم.

توی این پست قراره بریم عمیق تو دل این نوسان‌گر کلاسیک، یه سری نکته‌هاشو بررسی کنیم و همچنین اندیکاتورهای مشتق‌شده ازش رو مرور کنیم.

معرفی

اندیکاتور RSI یا شاخص قدرت نسبی، یه نوسان‌گر نرمال‌شده (با محدوده مشخص) بین 0 تا 100 هست. هدفش اینه که نشون بده قیمت کی تو محدوده اشباع خرید قرار داره (یعنی وقتی یه دارایی بالاتر از ارزش واقعی خودش معامله می‌شه) یا اشباع فروش (وقتی یه دارایی پایین‌تر از ارزش واقعی خودش معامله می‌شه) و چه زمانی ممکنه یه برگشت قیمتی اتفاق بیفته.

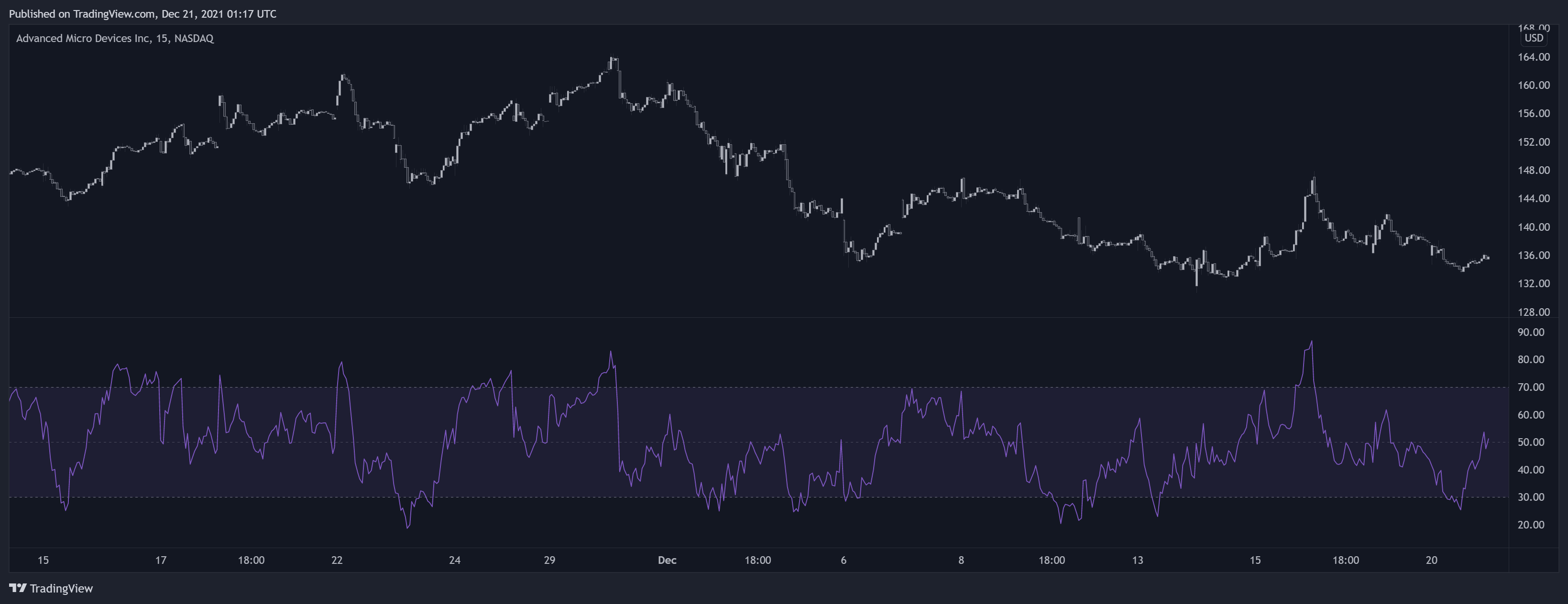
برای اینکه بفهمیم یه دارایی کی تو محدوده اشباع خرید یا اشباع فروش هست، اندیکاتور RSI از دو سطح ثابت استفاده می‌کنه:

• سطح اشباع خرید: 70 (که وایلدر پیشنهاد داده).
• سطح اشباع فروش: 30 (که وایلدر پیشنهاد داده).

اگه مقدار RSI بره بالای سطح 70، یعنی دارایی تو محدوده اشباع خرید قرار گرفته.
اگه مقدار RSI بیاد زیر سطح 30، یعنی دارایی تو محدوده اشباع فروش هست.

اندیکاتور RSI یه تنظیم به اسم طول دوره داره که کاربر می‌تونه باهاش تغییرات قیمت رو تو بازه‌های زمانی کوتاه‌تر یا بلندتر بررسی کنه.

این طول دوره معمولاً به‌صورت پیش‌فرض روی 14 تنظیم شده و اکثر مواقع هم تغییری توش داده نمی‌شه.

محاسبات

محاسبات مختلف برای RSI اطلاعات جالبی درباره نحوه ساخت این اندیکاتور و همچنین اطلاعاتی که این اندیکاتور قصد داره ارائه بده، نشان می‌ده.

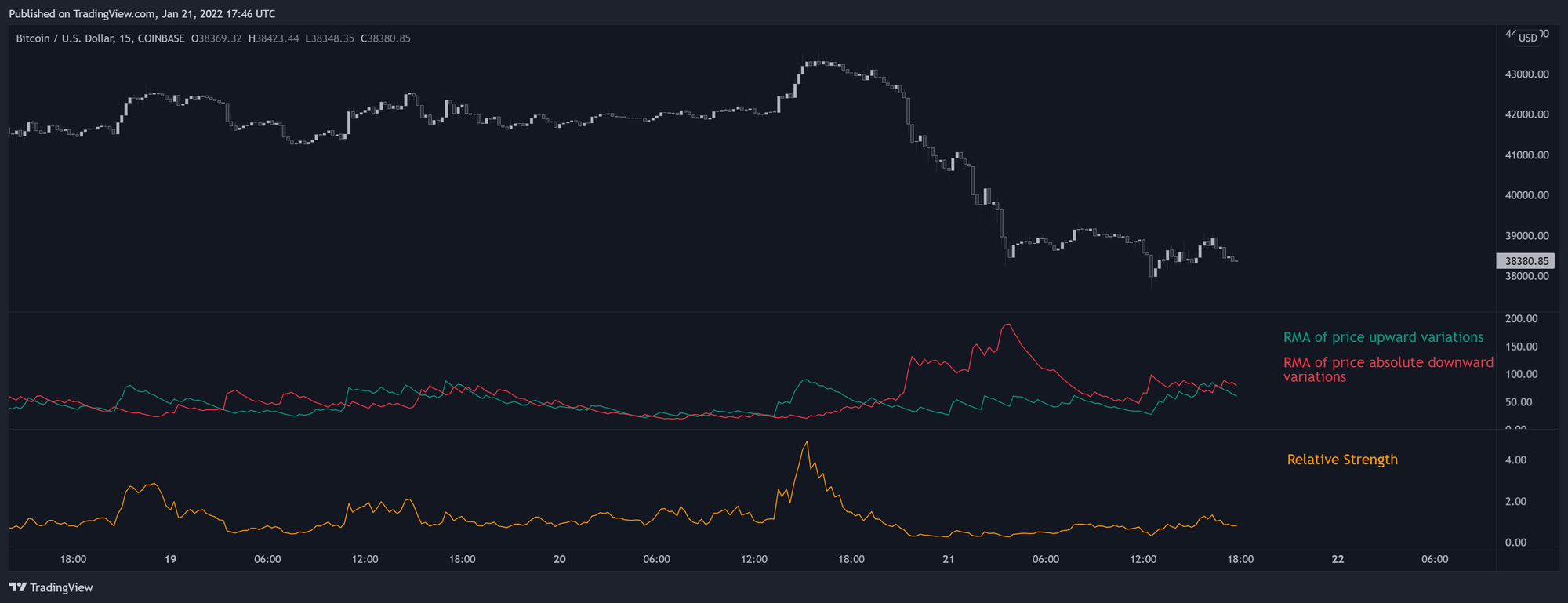
محاسبه‌ی RSI به طور کلی به این شکل انجام میشه:

delta = close - close[1]
upward = max(delta, 0)
downward = max(-delta, 0) 
relative_strength = rma(upward, length) / rma(downward, length)
relative_strength_index = 100 - 100 / (1 + relative_strength)

اینجا:

• close به قیمت بسته شدن اشاره داره.
• relative_strength همون قدرت نسبی رو نشون می‌ده.
• rma یا میانگین متحرک وایلدر (RMA) هست که به عنوان میانگین متحرک هموار شده (SMMA) هم شناخته میشه. این میانگین یه فیلتر نمایی هست که از ثابت هموارکننده 1/length به جای 2/(length+1) در مورد میانگین متحرک نمایی استفاده می‌کنه.

محاسبه‌ای ساده‌تر برای RSI به این صورت است:

RSI = rma(upward, length) / rma(abs(delta), length) × 100

این فرمول به ما می‌گوید که RSI نسبت میانگین تغییرات مثبت قیمت به میانگین تغییرات کلی (مثبت و منفی) قیمت را به صورت درصدی نشان می‌دهد. به عبارت دیگه، اگر RSI بالا باشد، یعنی تغییرات مثبت قیمت نسبت به کل تغییرات بیشتره و ممکنه بازار اشباع خرید شده باشه. برعکس، اگر RSI پایین باشه، یعنی تغییرات مثبت کمتر از تغییرات کلیه و ممکنه بازار اشباع فروش شده باشه.

انتخاب نوع میانگین متحرک برای محاسبه RSI

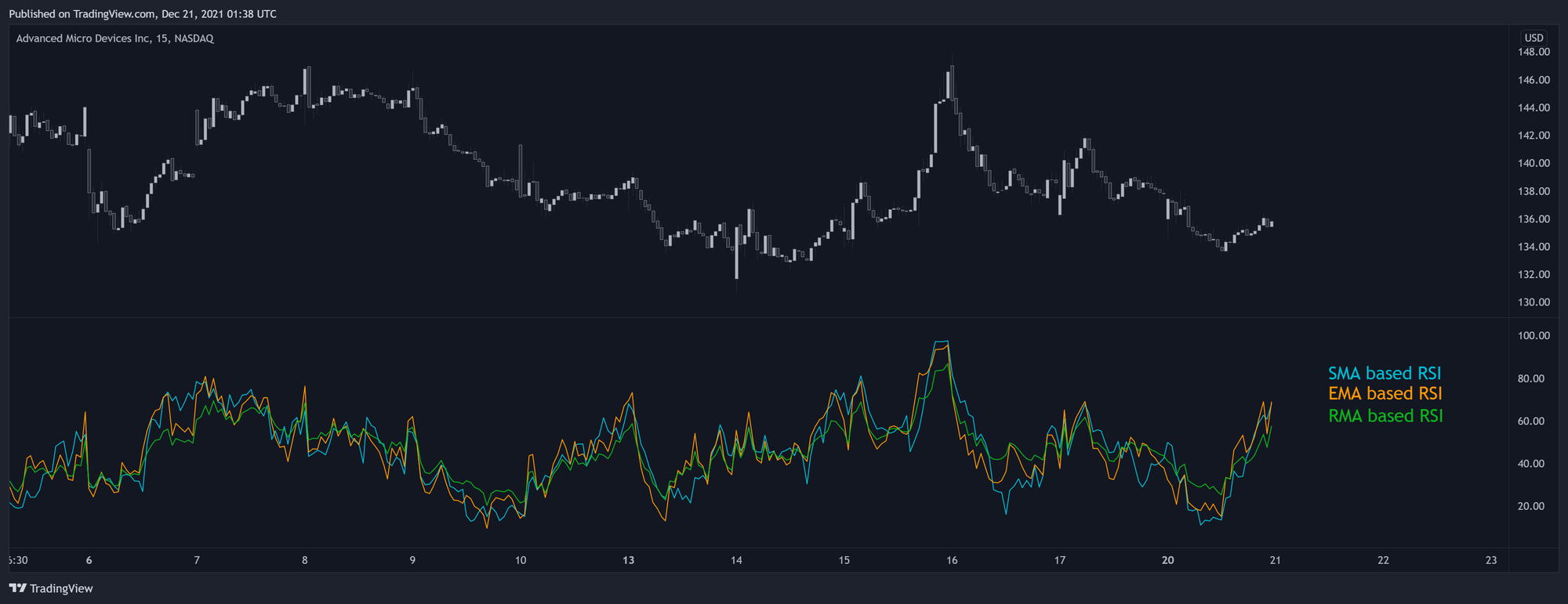
انتخاب نوع میانگین متحرک برای محاسبه RSI می‌تواند روی نتایج این اندیکاتور تأثیر بذاره و همچنین روش محاسبه‌اش رو تغییر بده.

محاسبه اصلی از میانگین متحرک وایلدر استفاده می‌کنه، اما نویسندگان مختلف ممکنه از میانگین متحرک ساده یا میانگین متحرک نمایی استفاده کنن.

نسخه کاتلر از RSI از میانگین متحرک ساده برای محاسبه RSI استفاده می‌کنه و تغییرات قابل توجهی رو نسبت به میانگین متحرک نمایی و وایلدر به همراه داره و چندین ویژگی خاص هم داره.

اول، محاسبه می‌تونه به شکل زیر به دست بیاد:

cutlers = (close - close[length])/length/MA(abs(delta),length) × 50 + 50

که میشه به سادگی به این شکل نوشت:

cutlers = (close - close[length])/SUM(abs(delta),length) × 50 + 50

میانگین متحرک ساده (SMA) نسبت به میانگین متحرک وایلدر (RMA) واکنش‌پذیری بیشتری داره و در نتیجه RSI که بر اساس SMA محاسبه می‌شه، بیشتر به سطح‌های اشباع خرید و فروش می‌رسه نسبت به RSI که بر اساس RMA محاسبه شده.

علاوه بر این، یک ورودی جدید قدیمی‌ترین ورودی را در پنجره محاسبات SMA حذف می‌کنه. این می‌تونه تغییرات شدیدی در RSI به وجود بیاره، در مقایسه با RSI که بر اساس EMA/RMA محاسبه میشه و حافظه‌ی ورودی‌های قدیمی‌تر رو حفظ می‌کنه.

یکی از معایب استفاده از SMA اینه که ممکنه با مشکل تقسیم بر صفر مواجه بشیم. هرچند این احتمال کم هست، اما اگر قیمت یک دارایی برای مدت بیشتری از مقدار قبلی خودش برابر باشه، این می‌تونه باعث بشه که تغییر قیمت 0 بشه، که در نهایت می‌تونه باعث بشه مخرج محاسبه قبلی برابر با 0 بشه. این مشکل مستقیماً وقتی که از فیلترهای نمایی برای محاسبه RSI استفاده می‌کنیم پیش نمیاد.

استفاده از میانگین متحرک نمایی (EMA) بر خلاف SMA، تغییرات خاص و قابل توجهی رو به همراه نداره. RSI که بر اساس EMA محاسبه می‌شه نسبت به RSI که بر اساس RMA محاسبه شده، واکنش‌پذیری بیشتری داره وقتی که از یک تنظیم طولی مشابه استفاده می‌کنیم. با این حال، هم EMA و هم RMA بر اساس میانگین‌گیری نمایی هستند و تنها ثابت هموارکننده متفاوت است. بنابراین، برای به دست آوردن تنظیم طولی که در RSI بر اساس EMA استفاده می‌شه و برابر با RSI بر اساس RMA باشه، باید معادله زیر رو نسبت به len_ema حل کنیم:

1/len_rma = 2/(len_ema+1)
          = 2 × len_rma - 1

بنابراین، یک RSI که بر اساس EMA با طول ۲۷ محاسبه شده برابر با یک RSI که بر اساس RMA با طول ۱۴ محاسبه شده است.

اثر تنظیم طول بر روی RSI

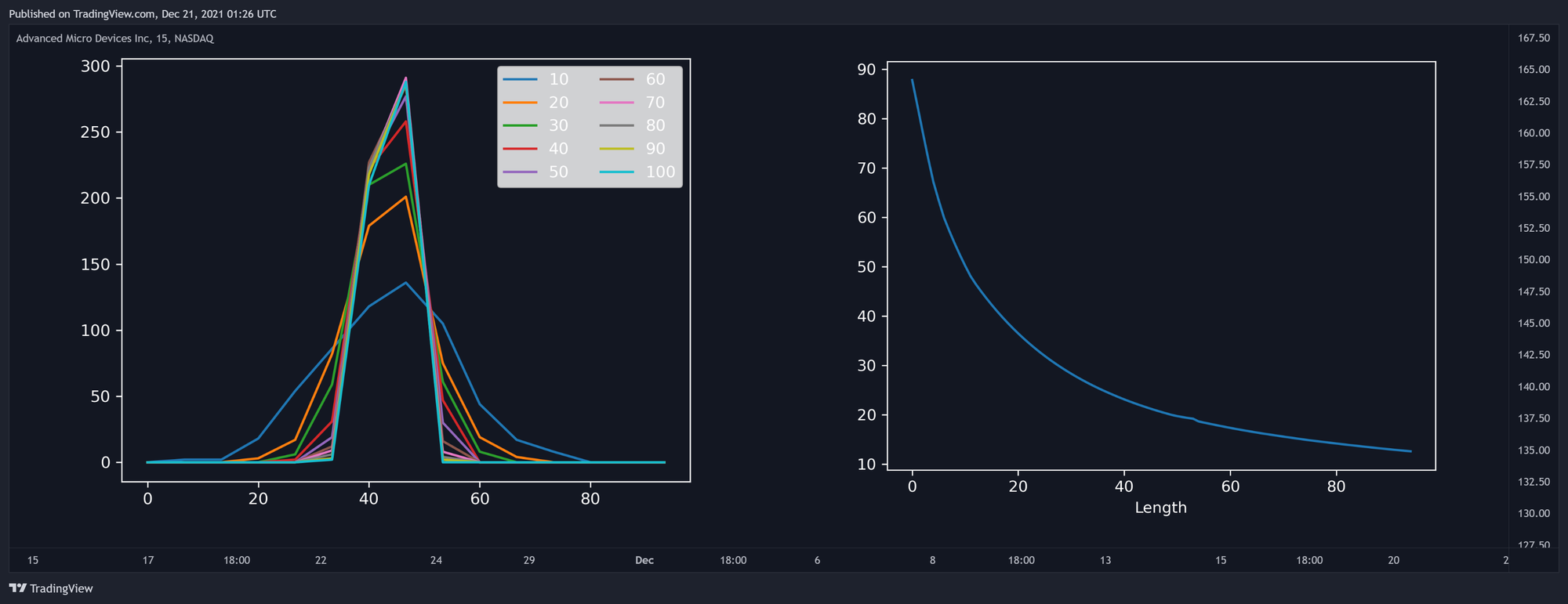
وقتی که RSI رو به بعضی از دارایی‌ها با اندازه نمونه بزرگ اعمال می‌کنیم، استفاده از یک تنظیم طول بالاتر، نتایجی نزدیک‌تر به مقدار مرکزی ۵۰ برمی‌گردونه و در نتیجه، دامنه RSI باریک‌تر می‌شه.

در تصویر بالا، در سمت چپ، می‌تونید هیستوگرام‌های فراوانی (به صورت نمودار خطی) رو ببینید که با اندازه بین ۱۵ از خروجی‌های مختلف RSI شامل ۵۰۰ مشاهده و با تنظیم طول رو به افزایش تهیه شده‌اند. RSI‌هایی با تنظیم طول بالاتر، شکل باریک‌تری برمی‌گردونند و همه دارای یک قله نزدیک به ۵۰ هستند. در سمت راست، دامنه مقادیر خروجی‌های RSI رو می‌بینید که در طول تنظیم (از ۱۰ تا ۱۰۰) بررسی شده و دامنه به صورت غیرخطی کاهش پیدا می‌کنه.

این رفتار معمولاً زمانی اتفاق می‌افته که از اندیکاتور RSI برای تغییرات قیمت با توزیع تقریباً متقارن و میانگین صفر استفاده بشه که معمولاً همینه.

بنابراین، استفاده از تنظیمات طولی بالاتر باعث می‌شه که RSI کمتر به سطوح اشباع خرید و فروش برسه. این ویژگی، RSI رو از نوسان‌سازهایی مثل نوسان‌ساز تصادفی متمایز می‌کنه، چون دامنه مشاهده شده در این نوسان‌سازها تغییر نمی‌کنه و این موضوع باعث می‌شه RSI برای شناسایی احتمالی معکوس‌ها مناسب‌تر باشه.

تفسیرها

وایلدر راه‌های مختلفی برای تفسیر RSI رو توضیح می‌ده.

استفاده از سطوح

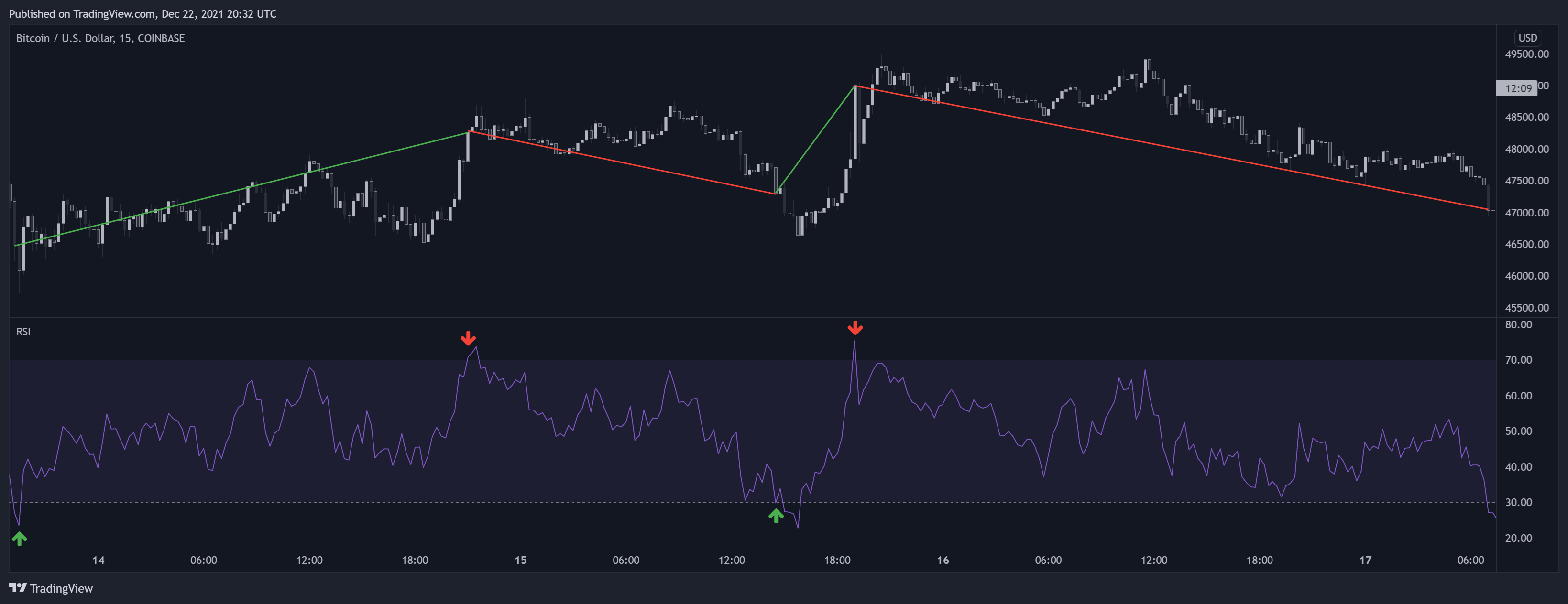
اصلی‌ترین تفسیر به تعامل بین RSI و سطوح اشباع خرید و اشباع فروش مربوط می‌شه. وقتی RSI بالای سطح اشباع خرید یا زیر سطح اشباع فروش باشه، نشون‌دهنده احتمال برگشت یا اصلاح قیمت هست. این علامت برگشت می‌تونه زمانی داده بشه که RSI از سطح اشباع خرید عبور کنه یا زیر سطح اشباع فروش بره. این کار به معامله‌گر اجازه می‌ده که زودتر به برگشت قیمت پی ببره، ولی ممکنه او رو در معرض ادامه روند قرار بده. از طرف دیگه، وقتی RSI زیر سطح اشباع خرید و بالای سطح اشباع فروش می‌ره، معامله‌گر کمتر در معرض ادامه روند قرار می‌گیره، ولی زمان‌بندی بهتری نداره.

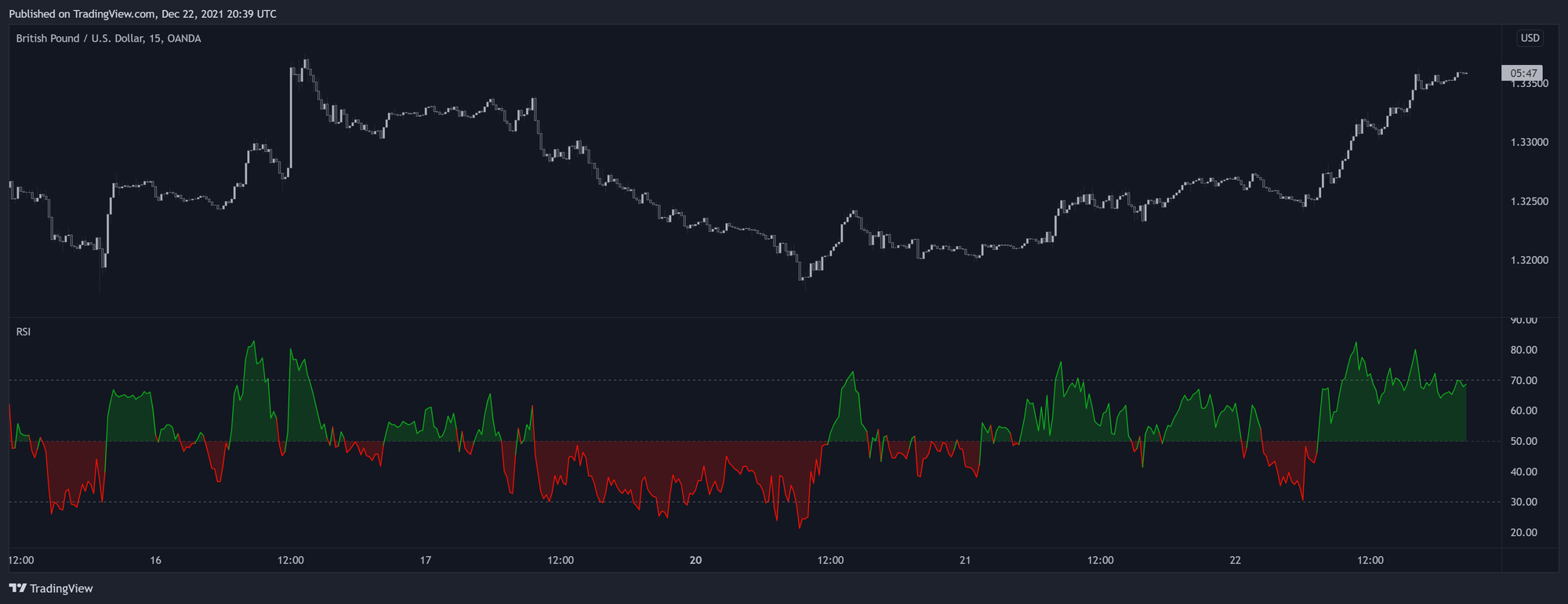
یک روش دیگه برای تحلیل RSI، استفاده از رویکردی پیرو روند هست. به این صورت که اگر RSI بالای 50 باشه، نشون‌دهنده یک روند صعودی و اگر زیر 50 باشه، نشون‌دهنده یک روند نزولی هست. هرچند این روش زمان‌بندی بهتری نداره و ممکنه باعث معامله‌های نوسانی بشه، اما به معامله‌گر اجازه می‌ده که روند بازار رو دنبال کنه به جای اینکه با اون مخالفت کنه.

شناسایی الگوها

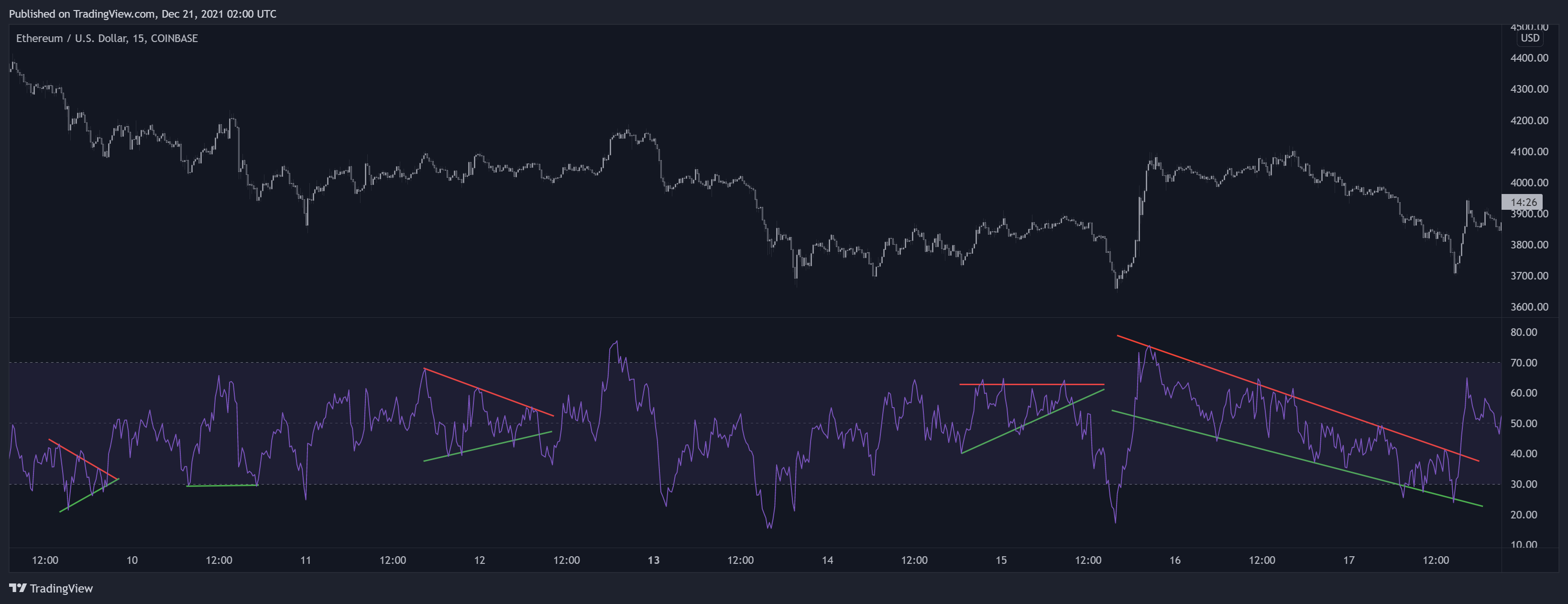
وایلدِر نشون می‌ده که الگوهای کلاسیکی مانند مثلث‌ها، گوه‌ها، سر و شانه‌ها و همچنین سطوح حمایت و مقاومت می‌تونن در RSI شناسایی و استفاده بشن. این شکل‌های قابل مشاهده نتیجه مشاهدات قیمتی بدون روند هستند که توسط RSI ارائه می‌شن و به همین خاطر ممکنه بیشتر هم دیده بشن. با این حال، طبیعت پرنوسان RSI ممکنه شناسایی این الگوها رو پیچیده‌تر کنه.

استفاده از واگرایی‌ها

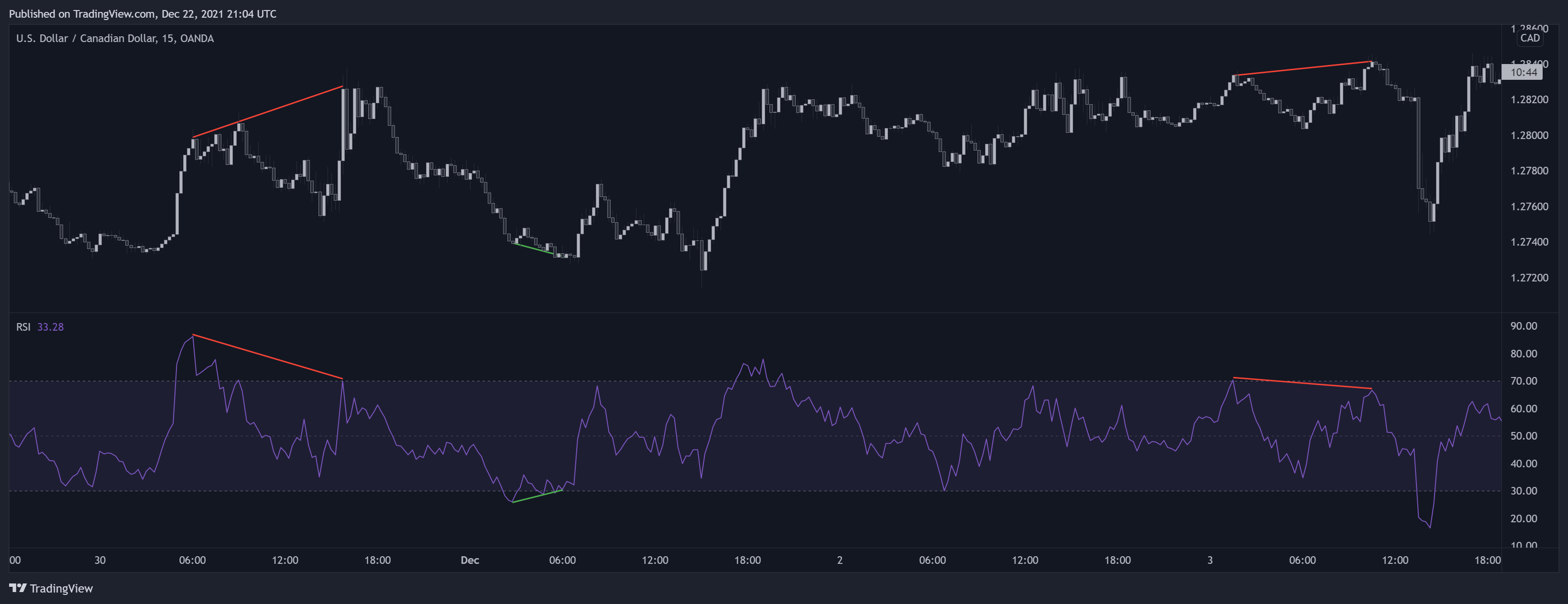
مثل اکثر نوسان‌نماها، واگرایی‌ها بین RSI و قیمت می‌تونن برای شناسایی نقاط برگشتی احتمالی استفاده بشن. واگرایی زمانی اتفاق می‌افته که اوج یا کف قیمت و اوج یا کف RSI به طور منفی همبسته هستن.

استفاده از نوسان‌های شکست

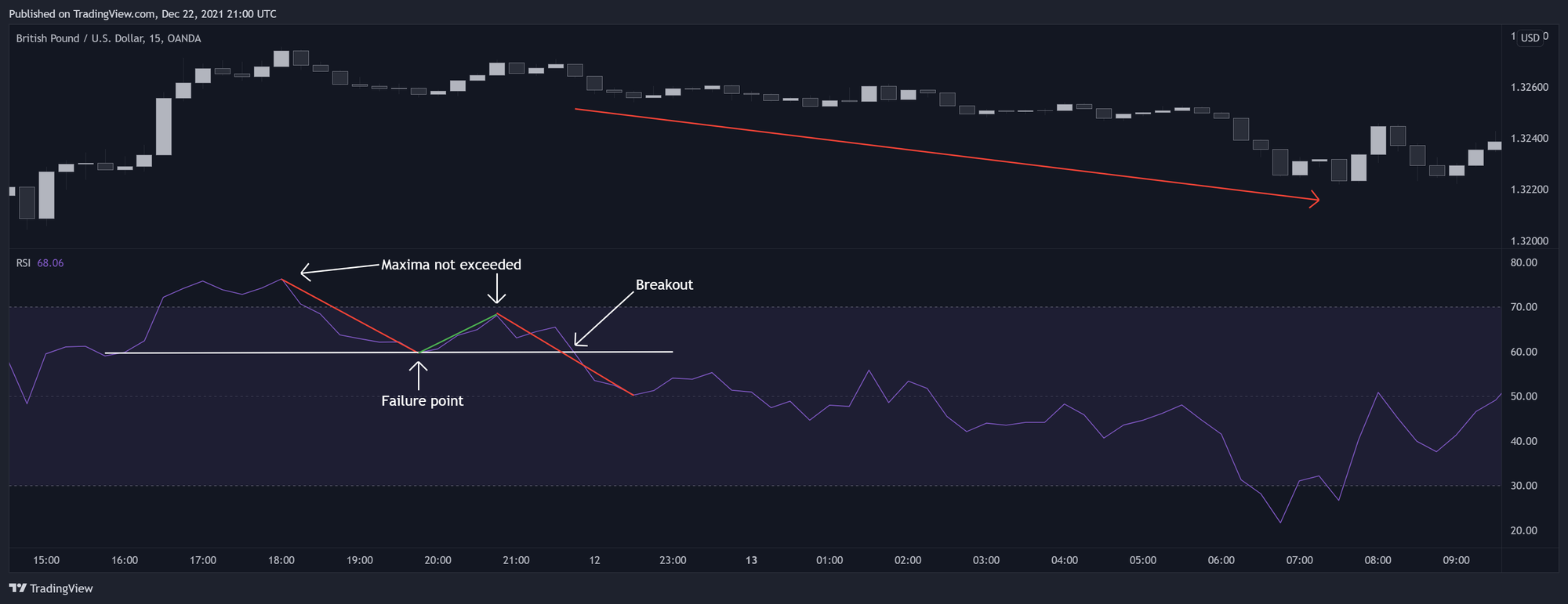
نوسان‌های شکست به این صورت تعریف می‌شن که RSI یک اوج یا کف قابل توجه بالای سطح اشباع خرید یا زیر سطح اشباع فروش ایجاد می‌کنه و بعد از اون یک اصلاح انجام می‌ده. سپس، RSI یک تلاش ناموفق برای رسیدن به سطح اشباع خرید یا فروش رو تجربه می‌کنه. نقطه شکست برای ورود به معامله تعیین می‌شه و این نقطه به حداکثر یا حداقل اصلاحی که بعد از اوج یا کف RSI اتفاق افتاده بستگی داره.

RSI دوره ۲ کانر

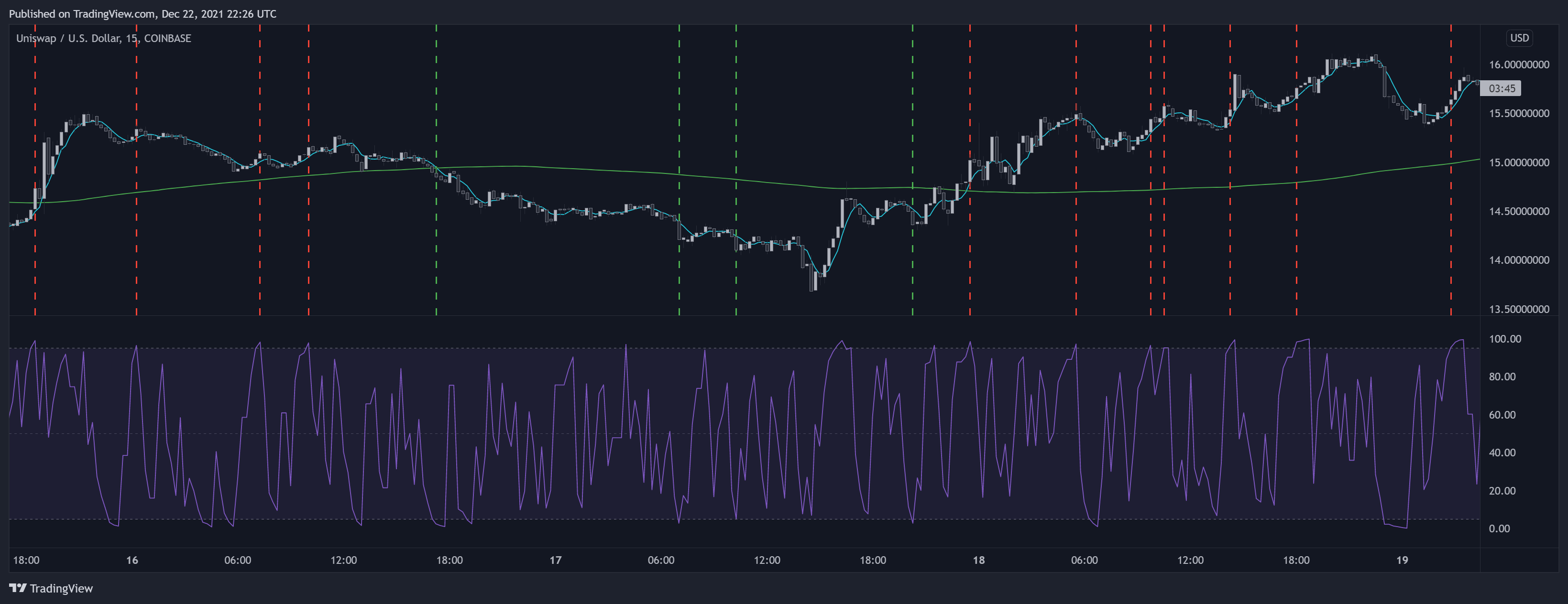
RSI دوره ۲ کانر یکی از استراتژی‌های کوتاه‌مدت و خلاف‌جهت هست که توسط لری کانرز توسعه داده شده و تفسیر متفاوتی از اندیکاتور RSI ارائه می‌ده. همونطور که از اسمش پیداست، این استراتژی بر اساس RSI با دوره ۲ بنا شده و بیشتر هدفش معامله بر روی اصلاحات و احتمال بازگشت‌های قیمتی هست. این استراتژی از یک میانگین متحرک با دوره ۲۰۰ برای تعیین روند کلی قیمت، از یک میانگین متحرک با دوره ۵ برای خروج و از RSI دوره ۲ برای ورود به معامله استفاده می‌کنه.

یک سفارش خرید وقتی باز می‌شه که RSI از زیر سطح اشباع فروش (که روی ۵ تنظیم شده) عبور کنه و قیمت زیر میانگین متحرک ساده ۲۰۰ دوره باشه. یه سفارش فروش هم وقتی باز می‌شه که RSI از بالای سطح اشباع خرید (که روی ۹۵ تنظیم شده) عبور کنه و قیمت بالای میانگین متحرک ساده ۲۰۰ دوره قرار داشته باشه. یک موقعیت هم وقتی بسته می‌شه که قیمت از بالای میانگین متحرک ساده ۵ دوره عبور کنه.

استفاده از چنین استراتژی‌ای نیاز به استفاده از تایم‌فریم‌های بالا داره تا از هزینه‌های اضافی ناشی از سودهای کوتاه‌مدت جلوگیری بشه.

دیگر اندیکاتورهایی که از RSI استفاده می‌کنند.

RSI در انواع مختلفی از اندیکاتورها استفاده می‌شود. در اینجا چند مورد از آن‌ها آمده است:

RSI تصادفی

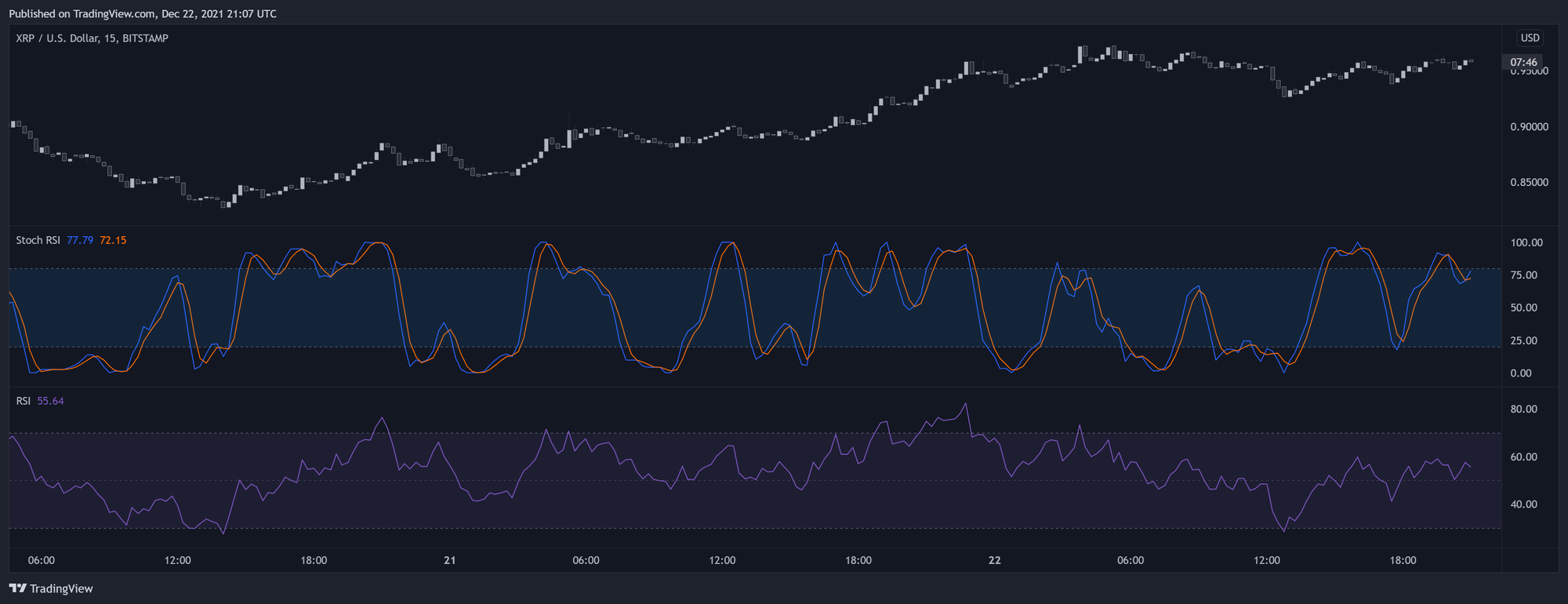
RSI تصادفی، همون‌طور که از اسمش پیداست، یه اسیلاتور تصادفی هست که از RSI به عنوان ورودی استفاده می‌کنه. از اونجا که RSI تغییرات قیمت رو پیش‌بینی می‌کنه، این باعث می‌شه که RSI تصادفی واکنش سریع‌تری داشته باشه. ماهیت محاسبات اسیلاتور تصادفی باعث می‌شه که RSI تصادفی در بازه (۰، ۱۰۰) قرار بگیره، که بر خلاف RSI، با افزایش طول RSI یا تصادفی به سمت ۵۰ نمی‌ره.

تحول معکوس فیشراهلرز

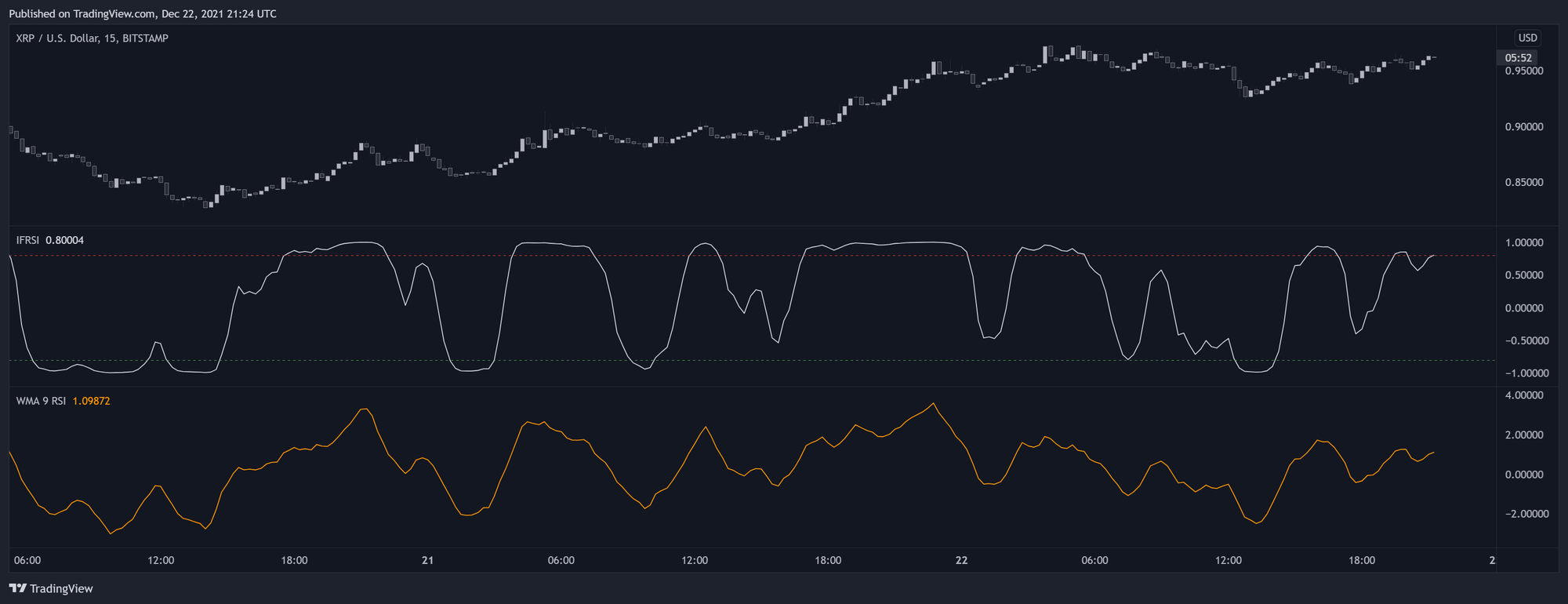
تحول معکوس فیشر (Ehlers Inverse Fisher Transform) توسط Ehlers در یک مقاله معرفی شده که این تبدیل به RSI صاف شده (میانگین وزنی متحرک با دوره ۹) اعمال می‌شه و در بازه (-۵، ۵) مقیاس‌بندی می‌شه. همان‌طور که قبلاً اشاره شد، RSI معمولاً توزیع متقارن و متمرکز بر روی ۵۰ داره. اعمال این تبدیل معکوس فیشر به RSI باعث می‌شه که توزیع به شکل U شکل دربیاد، به عبارت دیگه، RSI صاف شده اصلی "فشرده" می‌شه و نتیجه‌ای در مقیاس (-۱، ۱) برمی‌گردونه.

Laguerre RSI

RSI لاگور (Laguerre RSI) نسخه‌ای دیگه از RSI هست که Ehlers در مقاله‌ش به نام "Time Warp – Without Space Travel" ارائه می‌ده.

این اندیکاتور به طور مستقیم از RSI استفاده نمی‌کنه، بلکه شامل استفاده از فیلترهای چند مرحله‌ای هست که درجه‌ی نرمی اون‌ها با تنظیم کاربر به نام گاما در محدوده (۰، ۱) تعیین می‌شه. مقادیر گاما نزدیک‌تر به ۱، نشونه‌های بلندمدت‌تری رو برمی‌گردونن. برای محاسبه‌ی این اندیکاتور، صورت (نومیناتور) به عنوان مجموع اختلاف بین یک فیلتر و فیلتر بعدی در مرحله محاسبه می‌شه، و مخرج (دینامیناتور) مجموع اختلاف مطلق بین یک فیلتر و فیلتر بعدی در مرحله است. در نهایت، نسبت بین صورت و مخرج به محدوده (۰، ۱۰۰) مقیاس‌بندی می‌شه.

L0 = (1 - gamma) × close + gamma × L0[1]
L1 = -gamma × L0 + L0[1] + gamma × L1[1]
L2 = -gamma × L1 + L1[1] + gamma × L2[1]
L3 = -gamma × L2 + L2[1] + gamma × L3[1]
//----
num = (L0 - L1) + (L1 - L2) + (L2 - L3)
den = abs(L0 - L1) + abs(L1 - L2) + abs(L2 - L3)
lrsi = 50*num/den + 50

برخلاف RSI معمولی، Laguerre RSI با مقادیر بالای گاما به نزدیک 50 همگرا نمی‌شود و توزیع تقریبا به شکل U دارد.