میانگینهای متحرک یکی از اصول پایه تو دنیای تحلیل تکنیکاله و تو خیلی از شاخصهای فنی هم استفاده میشن. تو این پست، میخوایم سه نوع میانگین متحرک رو بررسی کنیم که معاملهگرها هر روز ازشون استفاده میکنن: میانگین متحرک ساده (SMA)، میانگین متحرک نمایی (EMA) و میانگین متحرک وزنی (WMA). بعضی از این موارد کاربرد عملی دارن و بعضیها هم فقط برای افزایش اطلاعات هستن.
مقدمه
میانگینهای متحرک بهعنوان شاخصهایی برای تشخیص روندها شناخته میشن و معمولاً برای هموار کردن تغییرات قیمت استفاده میشن، یعنی کمک میکنن که نوسانات قیمت رو کمتر کنیم و راحتتر بتونیم روند کلی رو ببینیم. استفاده از میانگینهای متحرک به سال ۱۸۲۹ برمیگرده، وقتی که جان فینلایسون از این روش برای هموار کردن نرخ مرگ و میر استفاده کرد!
تو تحلیل تکنیکال، میانگینهای متحرک یکی از ابزارهای پایه هستن که هر معاملهگری بهشون نیاز داره و تو هر نرمافزاری هم پیدا میشن. ولی این ابزارها فقط به بازارهای مالی محدود نمیشن و تو تحلیل دادههای سری زمانی و حتی پردازش سیگنالهای دیجیتالی هم کاربرد دارن.
میانگینهای متحرک تنظیماتی دارن که بهشون میگن "طول" یا "دوره" (یا بعضی وقتها "اندازه پنجره") و این تنظیمات مشخص میکنن که چقدر داده رو تو محاسبهاشون دخالت بدن تا میزان همواری یا نوسانشون تنظیم بشه.
کنجکاویهایی درباره میانگین متحرک ساده
میانگین متحرک ساده، که به اسم "SMA" هم شناخته میشه، یکی از پرکاربردترین و معروفترین میانگینهای متحرکه، چون هم ساده است و هم کاربرد زیادی داره. بهش میانگین متحرک حسابی هم میگن. تو محاسبه SMA، طول دوره مهمه و به این شکله که به همه دادهها وزن یکسان داده میشه. به همین خاطره که میگیم SMA وزنهای یکنواخت داره، چون هر داده بهطور مساوی تو میانگین حساب میشه.
رابطه با نوسانسنج مومنتوم
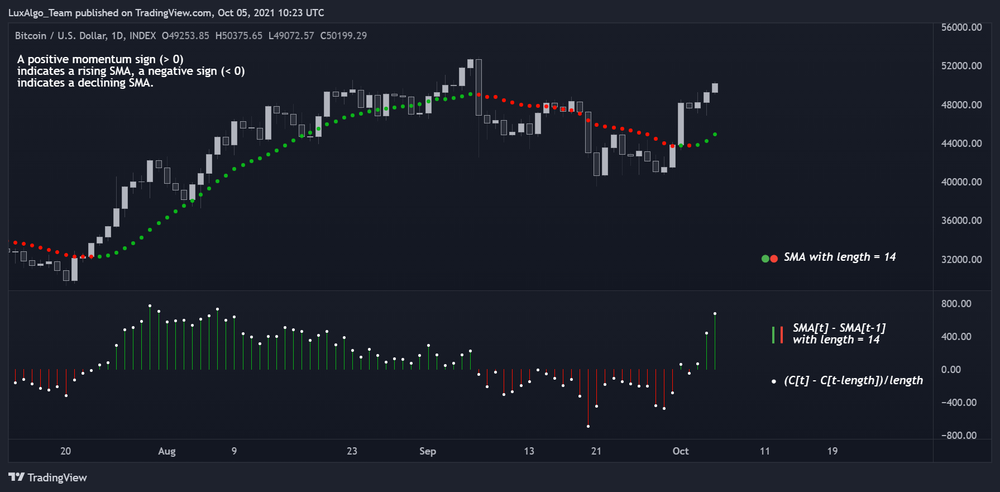
تغییرات در میانگین متحرک ساده (SMA) با طول دوره مشخص، مشابه نوسانسنج مومنتوم همون دوره است، البته وقتی که نتیجه نوسانسنج بر طول دوره تقسیم بشه. به این صورت میشه که با استفاده از محاسبه تغییرات در SMA، این موضوع رو راحتتر توضیح داد.
قیمتهای پایانی با تأخیر یکسان یکدیگر را خنثی میکنند و تنها C(t) و C(t-length) تقسیم بر طول در محاسبه نهایی باقی میماند.
پس میشه خیلی راحت فهمید که آیا میانگین متحرک ساده (SMA) در حال بالا رفتنه یا پایین اومدن، فقط کافیه قیمت پایانی امروز رو با قیمت پایانی چند دوره قبل مقایسه کنیم. اگر قیمت فعلی بالاتر باشه، یعنی SMA داره رشد میکنه و اگه پایینتر باشه، یعنی داره کاهش پیدا میکنه. این رابطه کمک میکنه تا محاسبه SMA سریعتر و مستقل از طول دوره انجام بشه، که این موضوع برای استفادههای لحظهای و کاربردهای با فرکانس بالا خیلی مهمه.
تأخیر میانگین متحرک ساده (SMA)
تأخیر توی میانگینهای متحرک یعنی این که این ابزار به جای اینکه بلافاصله تغییرات جدید قیمت رو نشون بده، تغییرات گذشته رو بازتاب میده. برای بیشتر میانگینهای متحرک، میشه این تأخیر رو با توجه به وزن هر دوره و تأخیر زمانیشون محاسبه کرد. اگه به قیمتهای جدیدتر وزن بیشتری بدیم، میانگین متحرک تأخیر کمتری داره. در مورد میانگین متحرک ساده، چون وزن همه دورهها یکیه و برابر با ۱/طول، تأخیرش میشه دوره زمانی منهای ۱، تقسیم بر ۲.
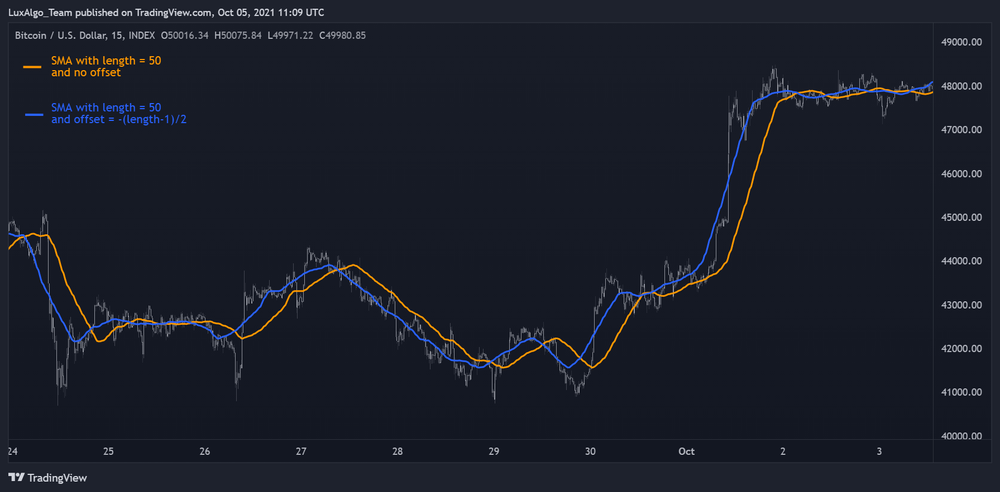
میانگینهای متحرک ساده متوالی (Cascaded SMAs)
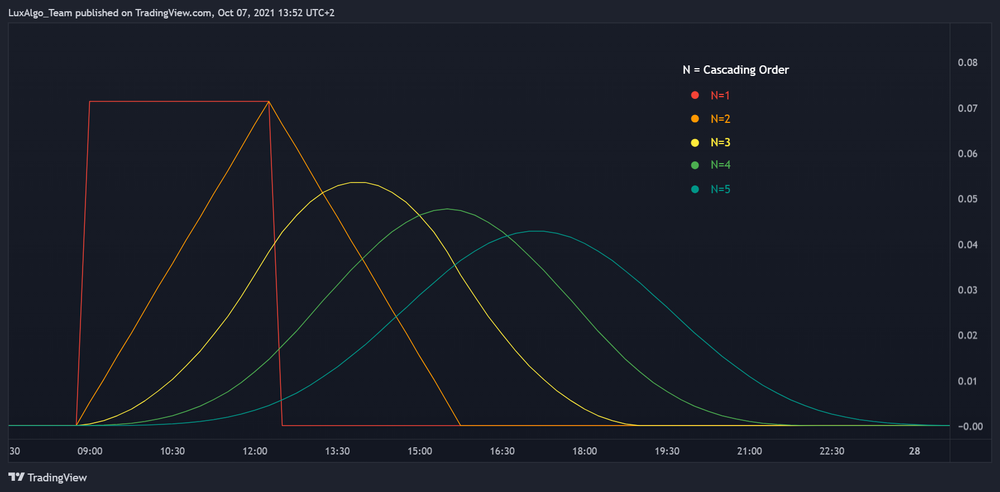
وقتی از یک میانگین متحرک ساده (SMA) بهعنوان ورودی برای یک میانگین متحرک ساده دیگه استفاده کنیم، خروجی صافتر و یکنواختتری میگیریم که به این روش "cascade" میگن. اگه چند تا SMA با دورههای یکسان رو پشت سر هم cascade کنیم، نتیجه به چیزی شبیه یه منحنی گاوسی (یه نوع منحنی صاف و زنگولهای) نزدیک میشه. در این حالت، تابع چگالی احتمال ایروین-هال میتونه این خروجیهای cascade رو با یه پالس ورودی توصیف کنه.
کنجکاویها درباره میانگین متحرک نمایی (EMA)
میانگین متحرک نمایی که بهش "EMA" هم میگن، یا به اسمهای "میانگین متحرک وزنی نمایی" و "میانگین نمایی" هم شناخته میشه، یه نوع میانگین متحرکه که تو محاسباتش از دادههای قبلی هم کمک میگیره. این مدل نسبت به میانگین متحرک ساده سریعتر به تغییرات قیمت واکنش نشون میده، چون کمتر تغییرات قیمت رو فیلتر میکنه.
معامله گران میانگین متحرک نمایی (EMA) را به میانگین متحرک ساده (SMA) ترجیح میدهند
به نظر میرسه که معاملهگرها بیشتر از میانگین متحرک نمایی (EMA) نسبت به میانگین متحرک ساده (SMA) استقبال میکنن. دلیل این موضوع میتونه به خاطر واکنش سریعتر EMA باشه که به تغییرات قیمت حساستره. به همین خاطر، EMA تو ساخت شاخصهای فنی بیشتر استفاده میشه؛ حالا یا به خاطر واکنشپذیری بالاترش، کارایی بهترش، یا حتی صرفاً چون بعضیها باهاش راحتترن.
چندین تحقیق سعی کردن بفهمن کدوم میانگین متحرک بهتر عمل میکنه. نتایجشون با توجه به بازارها و روشها متفاوت بوده. مثلاً دزیکویچوس و شاراندا EMA رو بهتر از SMA دونستن، و پریدیپباِی هم گزارش داده که MACD مبتنی بر EMA نسبت به SMA عملکرد بهتری داشته.
میانگین متحرک نمایی (EMA) به جلوگیری از تقسیم بر صفر کمک میکند
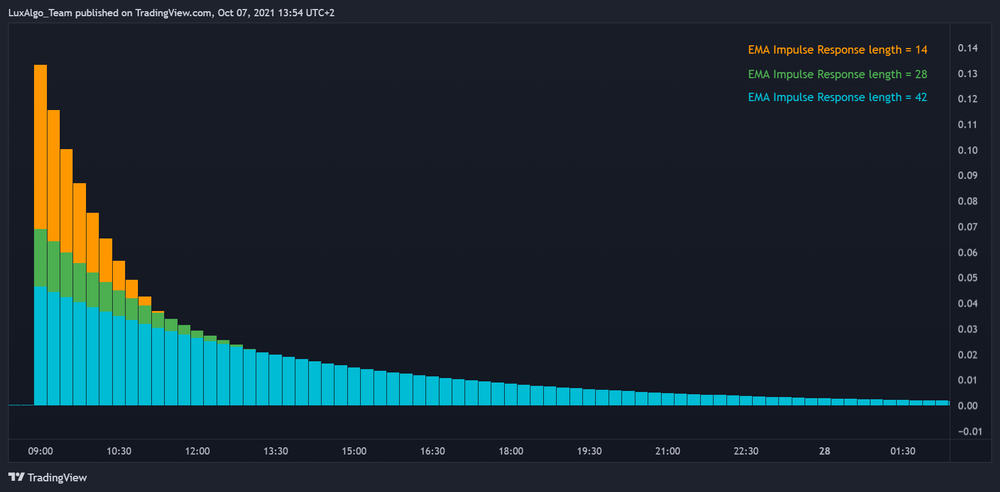
خب، اگر بخوایم توی محاسباتمون یه جایی تقسیم رو با میانگین متحرک نمایی (EMA) انجام بدیم، یه خوبی EMA اینه که احتمال تقسیم بر صفر رو تقریبا از بین میبره؛ به شرطی که ضریب هموارسازیش کمتر از ۱ باشه (یعنی دوره EMA بیشتر از ۱ باشه). چرا؟ چون EMA به شکلی طراحی شده که به مرور به سمت صفر میل میکنه، ولی هیچوقت دقیقا به صفر نمیرسه.
این ویژگی EMA به درد مواقعی میخوره که میخوایم مثلاً نسبت رشدهای صعودی به رشدهای نزولی رو حساب کنیم. توی این موارد اگه تعداد تغییرات صعودی بالا باشه، SMA ممکنه تغییرات نزولی رو تا صفر پایین بیاره و به مشکل تقسیم بر صفر برسه؛ اما EMA جلوی این قضیه رو میگیره و صفر نمیشه.
در نهایت، EMA هم یه تأخیری مثل SMA داره. ولی چون EMA سریعتر به تغییرات واکنش نشون میده، میتونیم بگیم که تأخیرش کمتر حس میشه، هرچند اصولاً تأخیر کلیش از ترکیب وزنهای مختلف EMA و تأخیرهای مرتبط، شبیه همون تأخیر SMA درمیاد.
کنجکاویها درباره میانگین متحرک وزنی (WMA)
میانگین متحرک وزنی یا همون WMA که بعضی وقتها بهش LWMA هم میگن، توی بین میانگینهای متحرک (مثل SMA و EMA) از همه سریعتر واکنش نشون میده. توی محاسباتش، WMA به دادههای جدیدتر وزن بیشتری میده و از یه سری وزنهای خطی کاهشی استفاده میکنه. یعنی هرچی قیمتها جدیدتر باشن، تأثیر بیشتری توی نتیجه نهایی دارن.
رابطه با میانگین متحرک ساده (SMA)
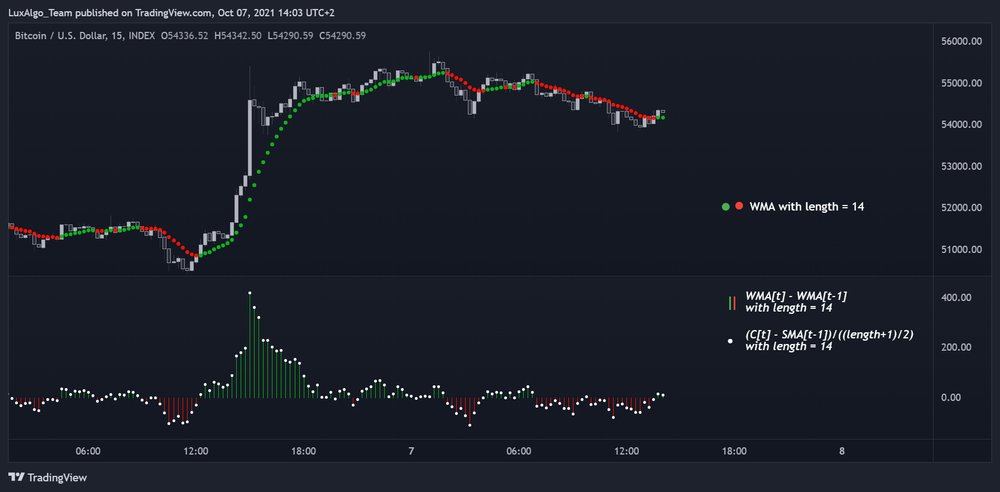
یه نکته جالب اینه که بعضی از میانگینهای متحرک به همدیگه ربط دارن. مثلاً WMA و SMA رو در نظر بگیر؛ میتونیم تغییرات WMA رو طوری حساب کنیم که بشه اختلاف قیمت با یه SMA (که به اندازه یه دونه کندل یا میله جابهجا شده) رو بگیریم و بعد اون اختلاف رو تقسیم بر یه عدد خاص کنیم (که اون عدد میشه طول دوره WMA + ۱ تقسیم بر ۲).
این رابطه به این شکل توضیح داده میشه:
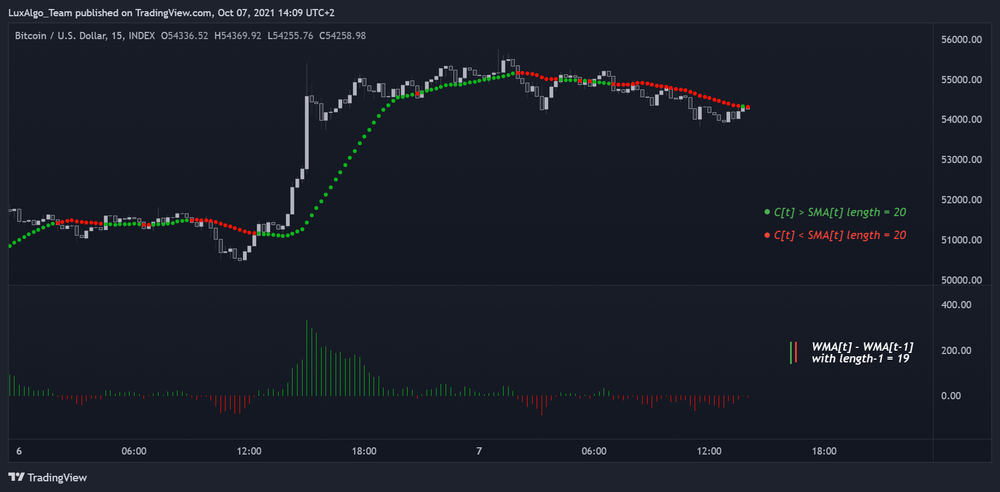
این رابطه به ما نشون میده که با تغییرات توی یه WMA با دورهای که یک واحد کمتره، میتونیم بفهمیم قیمت بالاتر یا پایینتر از یه SMA با همون دوره است. درست مثل SMA، این رابطه کمک میکنه که بتونیم WMA رو راحتتر حساب کنیم و زمان محاسبات رو طوری تنظیم کنیم که به طول دوره میانگین متحرک وابسته نباشه.
رابطه با رگرسیون خطی
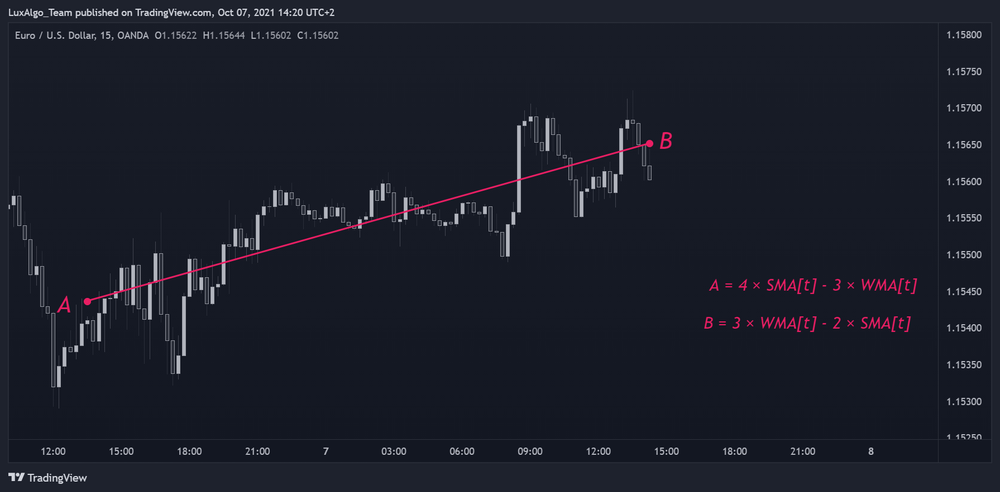
این شاید عجیب به نظر بیاد، ولی در واقع میشه یه رگرسیون خطی ساده از قیمتها رو با ترکیب خطی WMA و SMA (توی شرایط خاص) حساب کرد. رگرسیون خطی ساده اینجوری کار میکنه که نقطه اولش، که بهش (X1, Y1) میگیم، از جدیدترین قیمتها توی یه دوره مشخص بهدست میاد، و نقطه آخر هم با مختصات (X2, Y2) محاسبه میشه.
در این حالت، دوره WMA و SMA هر دو برابر با همون طول دوره هستن. حالا اگه یه خطی رو با این دو مختصات ترسیم کنیم، در واقع یه رگرسیون خطی ساده میسازیم که به جدیدترین قیمتهای دوره همخوانی داره. با همین مختصات هم میتونیم شیب این خط رگرسیون رو حساب کنیم.
